Maths 2nde / G4 - équations cartésiennes de droites

Questions :

Géométrie / G3 - Vecteurs colinéaires Apprentissage 0x Réussite 0/0

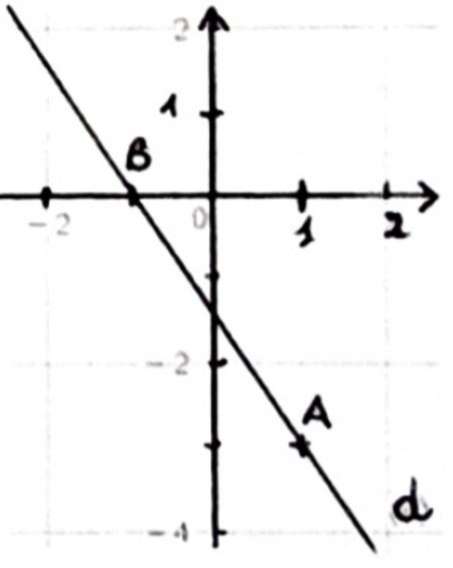
Qu'est-ce qu'un vecteur directeur d'une droite ?

C'est une vecteur non nul dont la direction est celle de la droite.

A savoir-faire :
Déterminer une équation cartésienne de droite ... MathAlea

Utiliser une équation cartésienne de droite pour ...

Déterminer les coordonnées d'un vecteur directeur d'une droite. MathAlea
Vérifier qu'un point appartient à une droite.
Calculer les coordonnées d'un point appartenant à une droite. MathAlea
Tracer la droite dans un repère. MathAlea
Vidéo

Utiliser les équations de deux droites ...

Déterminer si les droites sont parallèles ou sécantes. MathAlea
Calculer les coordonnées du point d'intersection de deux droites sécantes.

On se place dans un repère orthonormé

(O, i ⃗, j ⃗)

du plan.

1. Rappels

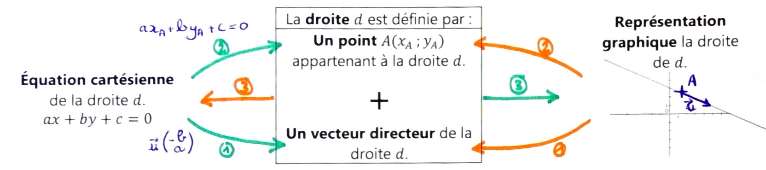
Définition : On appelle vecteur directeur de la droite

d

tout vecteur non nul

u ⃗

dont la direction est celle de la droite

d

.

Propriété : Soit $d$ la droite de vecteur directeur $\vec{u}$ et passant par un point $A$.
Un point $M$ appartient à la droite $d$ si et seulement si les vecteurs $\overrightarrow{AM}$ et $u ⃗$ sont colinéaires.

2. Equation cartésienne

A quelle condition sur ses coordonnées un point appartient-il à une droite ?

Soit

d

la droite passant par le point

A (- 2; 1)

et de vecteur directeur

u ⃗ (\begin{matrix} 5 \\ - 4 \end{matrix})

.
Un point

M (x; y)

appartient à la droite

d

⇔ les vecteurs

\vec{A M}

et

u ⃗

sont colinéaires.

⇔ les coordonnées de $\vec{A M} (\begin{matrix} x + 2 \\ y - 1 \end{matrix})$ et $u ⃗ (\begin{matrix} 5 \\ - 4 \end{matrix})$ sont proportionnelles.
⇔ $5 (y - 1) = (- 4) (x + 2)$
⇔ $5 y - 5 = - 4 x - 8$
⇔ $4 x + 5 y + 3 = 0$

Cette condition est appelée une équation cartésienne de la droite

d

.

2.1. Propriété

Toute droite $d$ admet une équation de la forme $a x + b y + c = 0$ , appelée équation cartésienne de $d$ .
De plus, le vecteur $u ⃗ (\begin{matrix} - b \\ a \end{matrix})$ est un vecteur directeur de $d$ .

2.2. Méthodes

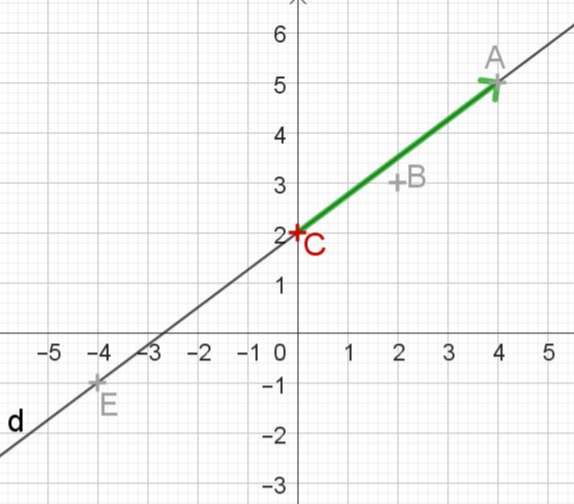
2.1.1. Déterminer une équation cartésienne de droite

Soit

d

la droite passant par le point

A (- 2; 1)

et de vecteur directeur

u ⃗ (\begin{matrix} - 5 \\ 4 \end{matrix})

.

$u ⃗ (\begin{matrix} - 5 \\ 4 \end{matrix}) = (\begin{matrix} - b \\ a \end{matrix})$ vecteur directeur de $d$ donc $d$ a pour équation $4 x + 5 y + c = 0$
$A (- 2; 1) \in d$ donc ses coordonnées vérifient l’équation $4 \times (- 2) + 5 \times 1 + c = 0$ ainsi $- 3 + c = 0$ soit $c = 3$ .

Conclusion : $d$ a pour équation $4 x + 5 y + 3 = 0$

Remarque : Une droite a une infinité d’équations cartésiennes.

Il suffit de multiplier les coefficients $a, b, c$ par un même réel non nul pour obtenir une autre équation cartésienne équivalente.
Dans l’exemple précédent, $- 4 x - 5 y - 3 = 0$ et $12 x + 15 y + 9 = 0$ sont d’autres équations cartésiennes de la droite $d$ .

2.2.2. Utiliser une équation cartésienne de droite

On considère la droite

d

d'équation

3 x - 4 y + 8 = 0

1. Les points $A (4; 5)$ et $B (2; 3)$ appartiennent-ils à $d$ ?
2. Le point $C$ d'abscisse $0$ appartient à $d$ . Quelle est son ordonnée ?
3. Déterminer les coordonnées d'un autre point de la droite $d$ .
Déterminer un vecteur directeur de la droite $d$ .
Tracer la droite $d$ dans un repère du plan.

1. - $3 \times 4 - 4 \times 5 + 8 = 12 - 20 + 8 = 0$
    Les coordonnées de $A$ vérifient l'équation de $d$ donc $A (4; 5) \in d$
  - $3 \times 2 - 4 \times 3 + 8 = 6 - 12 + 8 = 2 \neq 0$
    Les coordonnées de $B$ ne vérifient pas l'équation de $d$ donc $B (2; 3) \notin d$
2. $C (0; y) \in d$ donc ses coordonnées vérifient l'équation de $d$
  $3 \times 0 - 4 \times y + 8 = 0$ ainsi $- 4 \times y + 8 = 0$ soit $y = \frac{- 8}{- 4} = 2$ donc $C (0; 2)$
3. On choisit une abscisse $x$ et on cherche une ordonnée $y$ pour laquelle l'équation de $d$ est vérifiée.
  Si $x = - 4$ alors $3 \times (- 4) - 4 \times y + 8 = 0$ ainsi $- 4 \times y - 4 = 0$ soit $y = \frac{4}{- 4} = - 1$ donc $E (- 4; - 1) \in d$

La droite $d$ a une équation de la forme $a x + b y + c = 0$ avec $a = 3$ et $b = - 4$ donc $\vec{u} (\begin{matrix} - b \\ a \end{matrix}) = (\begin{matrix} 4 \\ 3 \end{matrix})$ est un vecteur directeur de $d$

$C (0; 2) \in d$ et $\vec{u} (\begin{matrix} 4 \\ 3 \end{matrix})$ vecteur directeur de $d$ .

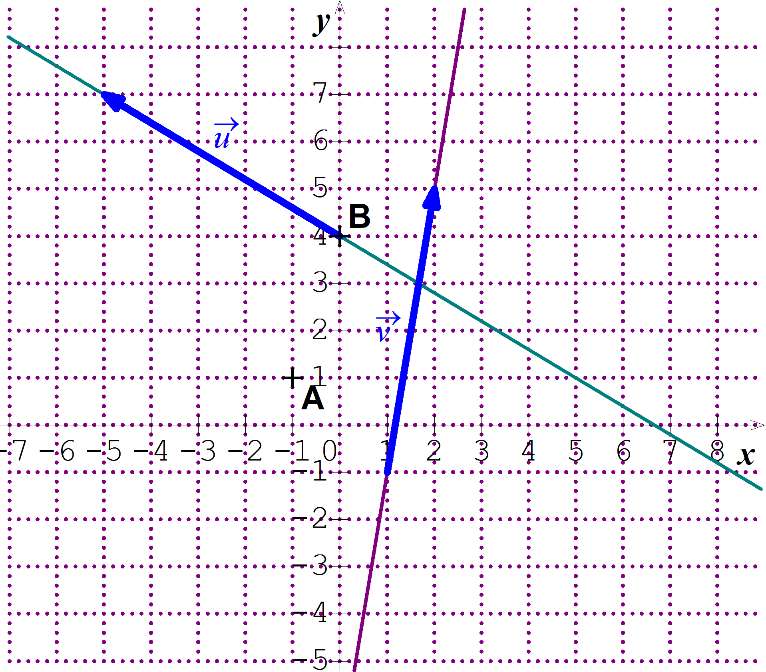
3. Droites sécantes

Propriété :

Deux droites sont sécantes si et seulement si leurs vecteurs directeurs ne sont pas colinéaires.
Le point d'intersection de deux droites sécantes est le point dont les coordonnées vérifient le système d'équations formé par les équations des deux droites.

On considère les droites

d

et

d^{'}

d'équations

3 x + 5 y - 20 = 0

et

6 x - y - 7 = 0

.

Vérifier que $d$ et $d^{'}$ sont sécantes.
Déterminer les coordonnées du point d'intersection de $d$ et $d^{'}$ .

Une droite d’équation $a x + b y + c = 0$ a pour vecteur directeur $\vec{u} = (\begin{matrix} - b \\ a \end{matrix})$
Ainsi, $\vec{u} = (\begin{matrix} - 5 \\ 3 \end{matrix})$ ) est une vecteur directeur de d et $\vec{v} = (\begin{matrix} 1 \\ 6 \end{matrix})$ ) est une vecteur directeur de d'.
$- 5 \times 6 \neq 3 \times 1$
Les coordonnées de $\vec{u}$ et $\vec{v}$ ne sont pas proportionnelles
donc $\vec{u}$ et $\vec{v}$ ⃗ ne sont pas colinéaires
donc $d$ et $d^{'}$ ne sont pas parallèles, ainsi $d$ et $d^{'}$ sont sécantes.

On remplace les coordonnées trouvées dans les deux équations :

3 \times \frac{5}{3} + 5 \times 3 - 20 = 5 + 15 - 20 = 0

et

6 \times \frac{5}{3} - 3 - 7 = 10 - 3 - 7 = 0

Les coordonnées trouvées vérifient les deux équations dont le point correspondant appartient bien aux deux droites

d

et

d^{'}

.