
Mesurer, c’est tout un art. La mesure est omniprésente dans notre quotidien : nous pesons nos ingrédients, nous mesurons des distances, des vitesses, des températures...
Généralement, des mesures approximatives nous suffisent, mais qu’en est-il lorsqu’on a besoin de garantir l’exactitude des mesures ?
« La métrologie, ou science de la mesure, rassemble l’ensemble des techniques permettant de réaliser des mesures, de les interpréter et d’assurer leur fiabilité.
Généralement, des mesures approximatives nous suffisent, mais qu’en est-il lorsqu’on a besoin de garantir l’exactitude des mesures ?
« La métrologie, ou science de la mesure, rassemble l’ensemble des techniques permettant de réaliser des mesures, de les interpréter et d’assurer leur fiabilité.
1. Processus de mesure et erreur
Le processus de mesure ou mesurage est l'ensemble des opérations qui permettent d'obtenir expérimentalement une ou plusieurs valeurs que l'on peut "raisonnablement" attribuer à une grandeur.
Le processus de mesure met en jeu :
- L'instrument de mesure
- L'opérateur (personne qui réalise la mesure)
- L'environnement (température, humidité, vibrations, .....)
- La méthode (protocole, étalonnage, ...)
Une mesure juste n'exite pas. Il est , par définition, impossible d'accéder à une valeur objective de la réalité sans erreur de mesure.
Il existe deux type d'erreur : l'erreur aléatoire et l'erreur systématique.
Il existe deux type d'erreur : l'erreur aléatoire et l'erreur systématique.
où est la moyenne des mesures en répétant fois le même processus de mesure avec
Ainsi l'erreur sera la somme d'un biais et d'une quantité aléatoire.
Lors d'un processus de mesure (ou mesurage) il est impossible d'obtenir la valeur vraie. Il y a toujours une erreur de mesure qui peut provenir :
- de la méthode choisie (un protocole peut être plus ou moins pertinent, ....)
- des instruments de mesures (l'affichage peut fluctuer, ou l'appareil est mal étalonné)
- de l'environnement (une mesure peut être sensible à la température de la pièce, par exemple)
- de l'opérateur (en TP vous êtes bien souvent la principale source d'erreur !)
Métrologie - Science de la mesure / Incertitudes
Apprentissage 0x
Réussite 0/0/2
Cocher les 2 erreurs aléatoires parmi les 4 propositions suivantes :
Cocher la ou les bonnes réponses.
Valider les quatre questions ci-dessus pour voir la suite.
2. Variabilité des mesures et incertitude-type
On réalise 100 mesures de l'éclairement. On obtient une série de valeurs : `E =130,2` lux ; `E =155,1` lux ; `E = 119,0` lux ; etc.
On recommence avec une série de 1000 mesures.
Pour y voir plus clair, on réprésente ces 100 mesures dans un histogramme avec en pointillé rouge, la valeur moyenne. La double flèche représente l'incertitude type de la mesure.
On recommence avec une série de 1000 mesures.
Pour y voir plus clair, on réprésente ces 100 mesures dans un histogramme avec en pointillé rouge, la valeur moyenne. La double flèche représente l'incertitude type de la mesure.

Moyenne 150,50 lux
Écart-type : 8,16 lux

Moyenne 148,30 lux
Écart-type : 8,01 lux
La dispersion des valeurs reflète l'impossibilité de connaître exactement la valeur d'une grandeur que l'on cherche à mesurer. D'après les histogrammes, on se doute que la valeur de l'éclairement est proche lux, mais pour donner un résultat scientifiquement valable, il faut se fixer une règle pour la valeur finale (on prendra la moyenne), et choisir une grandeur pour caractériser la dispersion des mesures (on prendra l'écart-type).
Pour une série de `N` mesurages `x_i` d'un grandeur `X` on note `barx=` la moyenne et `s(x_i)` ou `sigma` l'écart type expériemental.
Ces valeurs se calculent automatiquement avec une calculatrice ou un tableur.
`barm=1/Nsum_(i=1)^N x_i` et `s(x_i)=sigma=sqrt(1/(N-1)sum_(i=1)^N (x_i-barx)^2`
Sans incertitude il nous est impossible de comparer deux résultats ou de réfuter une loi. Pour qu'un résultat ait une valeur scientifique il faut pouvoir prouver que les éventuels écarts entre la théorie et l'expérience ne sont pas significatifs.
Pour une série de mesure, la valeur la plus probable est la moyenne. L'écart-type nous rensigne sur la dispersion des mesures causée par les erreurs de mesure.
Le résultat final d'une série de mesure d'une grandeur est exprimé sous la forme d’un intervalle de valeurs probables.
où est la moyenne de la série de mesure et l'incertitude-type.
3. Exactitude d'un mesurage
L'exactitude est le degré de proximité entre résultat du mesurage la mesure et la valeur vraie.Elle se décompose en :
justesse qui décrit l'erreur systématique ou biais statistique
fidélité qui décrit l'erreur aléatoire
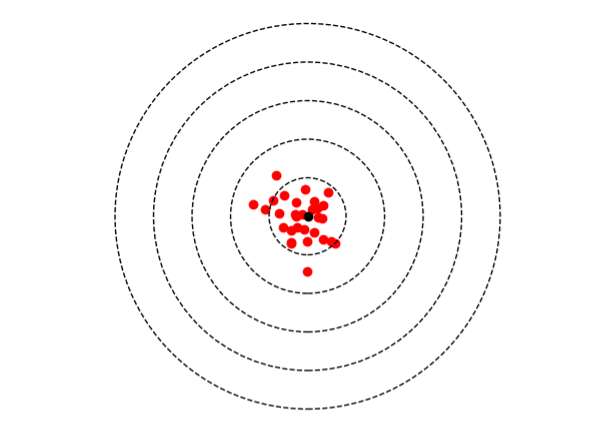
Juste et fidèle
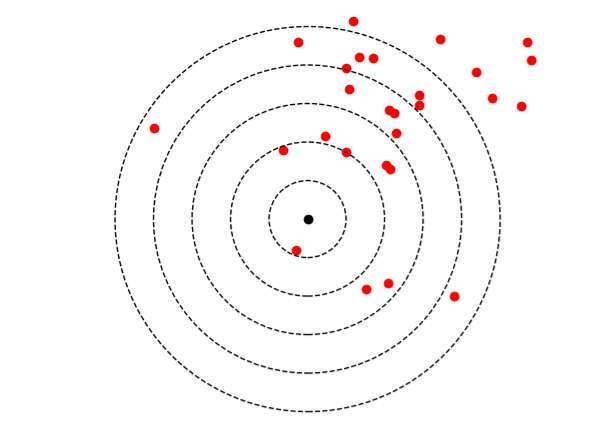
Ni juste, ni fidèle

Assez juste mais pas fidèle
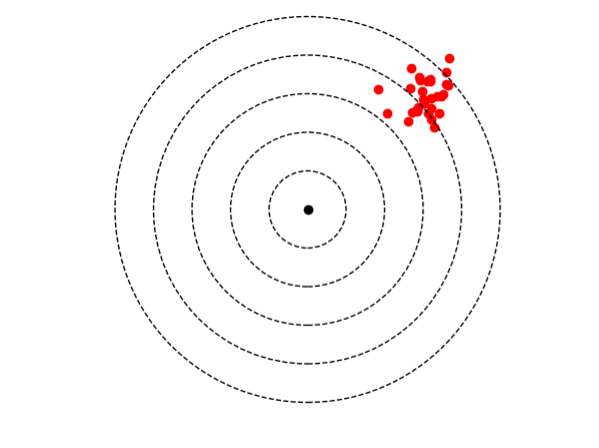
Fidèle mais pas juste
Métrologie - Science de la mesure / Incertitudes
Apprentissage 0x
Réussite 0/0
Question focus (Restez dans le cadre !)
Associer la cible à la bonne définition du mesurage
|
Mesurage ni juste ni fidèle
|
Mesurage fidéle mais pas juste
|
Mesurage juste mais pas fidèle
|
Mesurage juste et fidèle
|
|
|
|
|
|
Former les bons couples par glisser-déposer ou clics successifs.
Valider la question ci-dessus pour voir la suite.
4. Intervalle de confiance
On suppose que la répartition des mesures soit données par une loi normale (ou gaussienne) centrée sur la valeur moyenne des mesures d'écart-type .
La probabilité de mesurer une valeur est donnée dans la courbe de densité de probabilité.
Il y a 68 % de chance que la valeur mesurée soit dans l'intervalle bleu foncé (intervalle de confiance à 68%).
Avec l'intervalle bleu clair, cette probabilité passe à 95 % (intervalle de confiance avec un niveau de confiance de 95 %).
La probabilité de mesurer une valeur est donnée dans la courbe de densité de probabilité.
Il y a 68 % de chance que la valeur mesurée soit dans l'intervalle bleu foncé (intervalle de confiance à 68%).
Avec l'intervalle bleu clair, cette probabilité passe à 95 % (intervalle de confiance avec un niveau de confiance de 95 %).
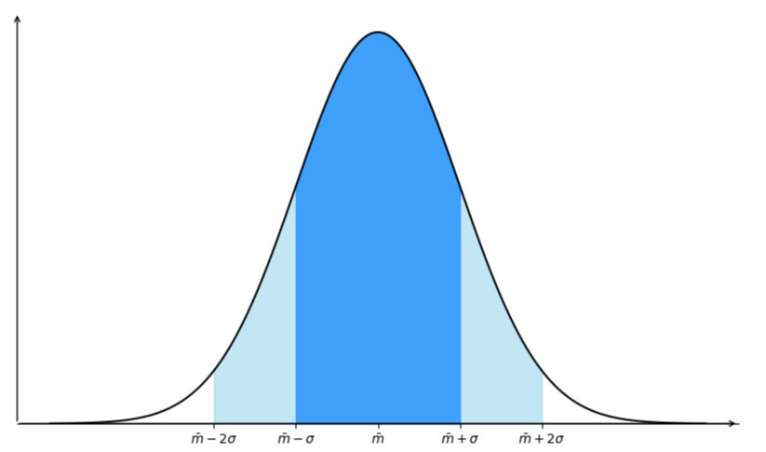
des valeurs sont dans l'intervalle
des valeurs sont dans l'intervalle
On introduit alors l'incertiude élargie . Elle est reliée à l'incertitude type par la relation :
où est appelé facteur d'élargissement.Le facteur permet de fixer, le niveau de confiance du mesurage.
Plus est grand et plus la probabilité de trouver la valeur vraie dans l'intervalle de confiance est élevé.
où est appelé facteur d'élargissement.Le facteur permet de fixer, le niveau de confiance du mesurage.
Plus est grand et plus la probabilité de trouver la valeur vraie dans l'intervalle de confiance est élevé.
3. Présentation du résultat
Chiffre significatif : Dans une valeur numérique, le premier chiffre non-nul de gauche désigne le chiffre le plus significatif et le dernier chiffre de droite le chiffre le moins significatif.
Le zéro a une situation particulière. Les zéros placés à gauche du premier chiffre différent de zéro ne sont pas significatifs, ceux placés à droite le sont.
Lorsqu'on effectue des calculs à partir de plusieurs valeurs, le nombre de chiffres significatifs du résultat doit être égal au nombre de chiffres significatifs le moins important des valeurs de départ.
Le nombre de chiffres significatifs sous-entends la précision avec laquelle une valeur est connue.
En effet, lorsque l'on écrit un résultat, seul le dernier chiffre significatif n'est pas connu avec certitude.
En effet, lorsque l'on écrit un résultat, seul le dernier chiffre significatif n'est pas connu avec certitude.
La surface vaut m2 mais le bon résultat est m2 (2 chiffres significatifs)
Il faut donc arrondir le résultat au centième.
Par exemple,
- arrondir
- arrondir
- arrondir
Si l'on reprend l'exemple précédent, l'écriture correcte du résultat est : m·s-1
Une fois l'incertitude estimée avec 1 ou 2 chiffres. On arrondi la valeur du résultat de la mesure de manière à ce que son dernier chiffre significatif soit à la même position décimale que celui de l'incertitude .
Le résultat se met sous la forme : unité unité
ou bien en écriture scientifique unité
Métrologie - Science de la mesure / Incertitudes
Apprentissage 0x
Réussite 0/0
Quelles affirmations concernant les chiffres significatifs sont correctes ?
Choisissez toutes les réponses correctes.
Cocher la ou les bonnes réponses.
Valider les sept questions ci-dessus pour voir la suite.
5. Comparaison de deux valeurs
5.1. Comparaison à une valeur de référence
On considère que la mesure est compatible avec la valeur de référence si le z-score est inférieur à 2.
Le seuil est une convention arbitraire.
Pour rappel, dans une distribution gaussienne, des valeurs sont dans l'intervalle , seulement des mesures ont un z-score supérieur à 2.
Si le z-score est proche de 2 cela signifie surtout qu'il faut améliorer le processus de mesure de manière à diminuer les incertitudes.
5.2. Comparaison de deux mesures entre elles
On considère à nouveau que les mesure sont compatibles si leur écart normalisé est inférieur à 2.