Header
🠖 Nombres et Calcul

N0 et N2-Développer Factoriser

Nombres et Calcul / C1-Développer et Factoriser Apprentissage 0x Réussite 0/0
Que signifie factoriser ?
Factoriser signifie transformer une somme en produit.
A savoir faire :
  1. reconnaître la structure d'une expression algébrique (somme, produit, priorités, etc...)
  2. développer, factoriser et réduire (sans identité remarquable)
    Entrainement MathAlea
  3. développer, factoriser et réduire (avec les identités remarquables)
    Entrainement MathAlea

1. Vocabulaire et premières propriétés

Définitions :
  • Développer consiste à transformer un produit en somme.
  • Factoriser consiste à transformer une somme en produit.
Définitions :
  • Une somme est le résultat d'une addition.
  • Un produit est le résultat d'une multiplication.
Propriété :
  • Une somme reste la même lorsque on change l'ordre des termes qui la compose.
  • Un produit reste la même lorsque on change l'ordre des facteurs qui le compose.
    $a+b=b+a$
    $a \times b=b \times a$
Notations :
x=1x −x=−1x xy=x×y x2=x×x
Propriété 1 :
  • Soustraire un nombre revient à ajouter son opposé.
  • Ajouter un nombre revient à soustraire son opposé.
    $a-b=a+(-b)$
    $a+b=a-(-b)$
Exemple 1 : La différence de $x$ et de $8$ est aussi la somme de $x$ et de $-8$ (l'opposé de $8$) $$x-8=x+(-8)$$
Exemple 2 : L'expression $-3x^2-5x-7$ peut être vue comme la somme des trois termes $-3x^2$, $-5x$ et $-7$. $$-3x^2-5x-7=-3x^2+(-5x)+(-7)$$
Le quotient de $x$ par $5$ est aussi le produit de $x$ par $\frac{1}{5}$ (l’inverse de $5$) $$ \frac{x}{5}=\frac{1}{5} \times x$$

2. Distributivité de la multiplication sur l'addition

Propriété :
  • Le produit de deux nombres positifs est un nombre positif.
  • Le produit de deux nombres négatifs est un nombre positif.
  • Le produit d'un nombre positif par un nombre négatif est un nombre négatif.
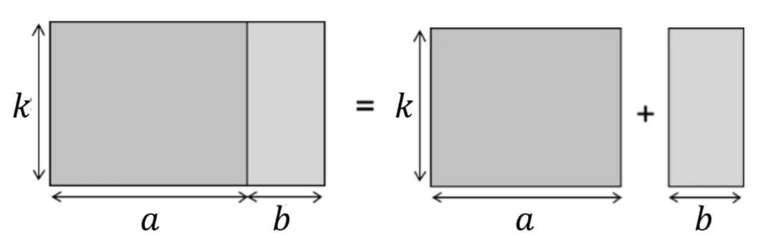
Propriété 2 : Distributivité simple
pour développer pour factoriser
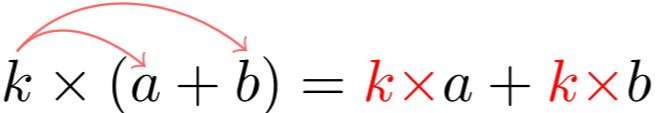$ \color{red}{k \times} \color{black}a + \color{red}{k\times} \color{black}b - \color{red}{k\times} \color{black}c= \color{red}{k \times}\color{black} (a+b-c)$
On distribue $k$ sur chaque terme de la somme. $k$ est un facteur commun commun aux termes de la somme.
et en particulier :
pour simplifier une expression avec un signe plus ou un signe moins précédant une somme entre parenthèses. pour réduire une somme
$+(somme)=+1 \times (somme)$
On distribue $1$ sur chaque terme de la somme.

$-(somme)=-1 \times (somme)$
On distribue $-1$ sur chaque terme de la somme.
Exemples :
Développer et réduire
$3x-(x+5)$
et
$7-(-8+2x²-9x)$
Réduire :
$8x^2-3+2x^2$
et
$x-5x+2x$
$\begin{align*} 3x-(x+5) & = 3x-1 \times (x+5) \\ & = 3x+(-1) \times (x+5) \\ & = 3x + (-1) \times x + (-1) \times 5 \\ & = 3x -x -5 \\ & = 2x -5 \end{align*}$
$\begin{align*} 7-(-8+2x²-9x) & = 7-1 \times (-8+2x²-9x) \\ & = 7+(-1) \times (-8+2x²-9x) \\ & = 7 + (-1) \times (-8) + (-1) \times 2x² + (-1) \times (-9x) \\ & = 7 + 8 - 2x² + 9x \\ & = 15 - 2x² + 9x \end{align*}$
$\begin{align*} 8x^2-3+2x^2 & = 8x^2+2x^2-3 \\ & = (8+2)x^2-3 \\ & = 10x^2-3 \end{align*}$
($x^2$ est le facteur commun aux deux termes $8x^2$ et $2x^2$)
$\begin{align*} x-5x+2x & = 1x-5x+2x \\ & = (1-5+2)x \\ & = -2x \end{align*}$
($x$ est le facteur commun aux trois termes $x$, $-5x$ et $2x$)

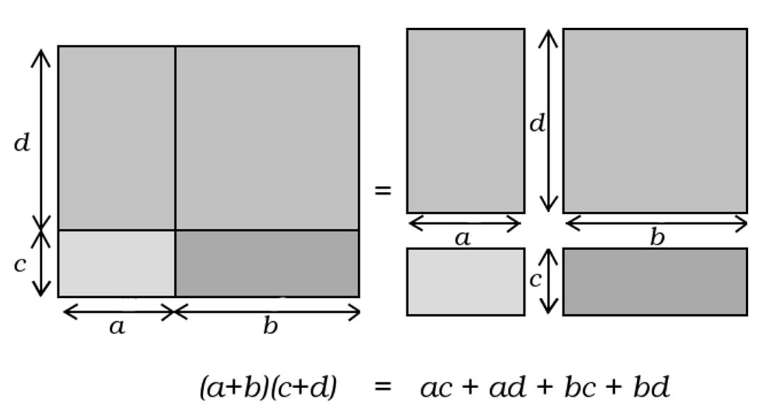
Propriété 3 : Double distributivité

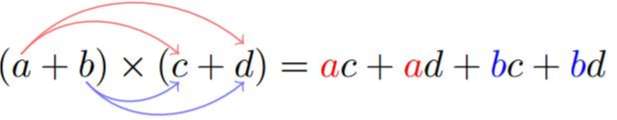
3. Identités remarquables

$3x^2$ est différent de $(3x)^2 $

$3x^2$ est le produit de $3$ et du carré de $x$ : $3x^2=3 \times x^2$
mais $(3x)^2$ est le carré de $3x$ : $(3x)^2=3x×3x=9×x^2=9x^2$

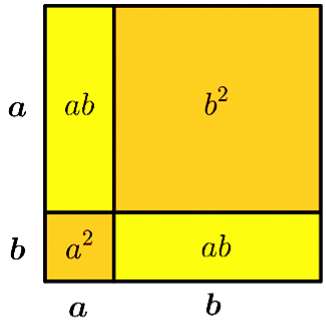
Propriété 4 : Identités remarquables

Le carré d'une somme ou d'une différence

⟶développer
(a+b)2=a2+2ab+b2
(a−b)2=a2−2ab+b2
⟵factoriser

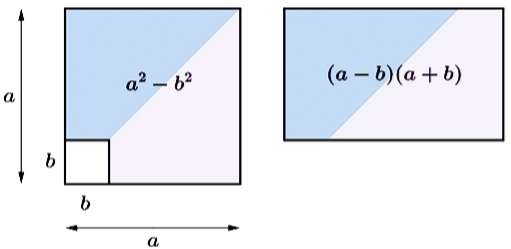
La différence de deux carrés

⟶factoriser
a2−b2=(a−b)(a+b)
⟵développer

Démonstration algébrique : $$\begin{align*} (a+b)^2 & = (a+b) \times (a+b) \\ & = a^2+ab+ba+b^2 \\ & = a^2+2ab+b^2 \end{align*}$$ Démonstration géométrique : L'aire du carré de côté $a+b$ est égale à la somme des quatres aires ci-dessous.
$\begin{align*} (a-b)^2 & = (a+(-b))^2 \\ & = a^2+2 \times a \times(-b)+b^2 \\ & = a^2-2ab+b^2 \end{align*}$
développer $(3x-4)^2$
développer $(7x+2)^2$
$\begin{align*} (3x-4)^2 & = (3x)^2-2×3x×4+4^2 \\ & = 9x^2-24x+16 \end{align*}$

$\begin{align*} (7x+2)^2 & = (7x)^2+2×7x×2+2^2 \\ & = 49x^2+28x+4 \end{align*}$
$\begin{align*} (a-b)(a+b) & = a^2+ab-ab-b^2 \\ & = a^2-b^2 \end{align*}$
Factoriser $25x^2-100$
Calculer mentalement $ 57 \times 63$
$\begin{align*} 25x^2-100 & = (5x)^2-10^2 \\ & = (5x-10)(5x+10) \end{align*}$ $\begin{align*} 57 \times 63 & = (60-3) \times (60+3) \\ & = 60² - 3² \\ & =3600-9 \\ & =3591 \end{align*}$