Header
🠖 Probabilités

P1 - Probabilités conditionnelles

A mémoriser :
Probabilités / Probabilités Conditionnelles Apprentissage 0x Réussite 0/0
Donner la formule de la probabilité conditionnelle $ P_A(B)= $
$ P_A(B)= \frac{P(A \cap B)}{P(A)}$
A savoir faire :
  • Calculer une probabilité conditionnelle
Probabilités / Probabilités Conditionnelles Apprentissage 0x Réussite 0/0
40 % des femmes jouent de la musique

F : "la personne est une femme"
M : "la personne est joue de la musique"
Traduire le nombre 0,4 en terme de probabilités.
$ 0,4=P_F(M) $
  • Changer de registre de langage (français vs notations mathématiques)
Probabilités / Probabilités Conditionnelles Apprentissage 0x Réussite 0/0
Que signifie le nombre 0,56 dans le tableau ci-dessous ?
$ P(B \cap S)=0,56 $
  • Construire un tableau croisé en lien avec une situation donnée
  • Exploiter un tableau croisé de données pour calculer des probabilités
Probabilités / Probabilités Conditionnelles Apprentissage 0x Réussite 0/0
Que signifie le nombre 0,4 dans l'arbre ci-dessous ?
$ P(A)=0,4 $
S'entrainer à la résolution de problème :

1. Déterminer une probabilité conditionnelle

A et B sont deux événements d’un univers donné de probabilité non nulle.
Définition : La probabilité de l’événement B sachant A est le nombre, noté PA(B), donné par :
PA(B)=P(A∩B)P(A)
Propriété (admise) : 0≤PA(B)≤1
Méthode pour déterminer une probabilité conditionnelle :
  • La calculer grâce à un tableau à double entrées.
  • La lire dans un arbre pondéré.

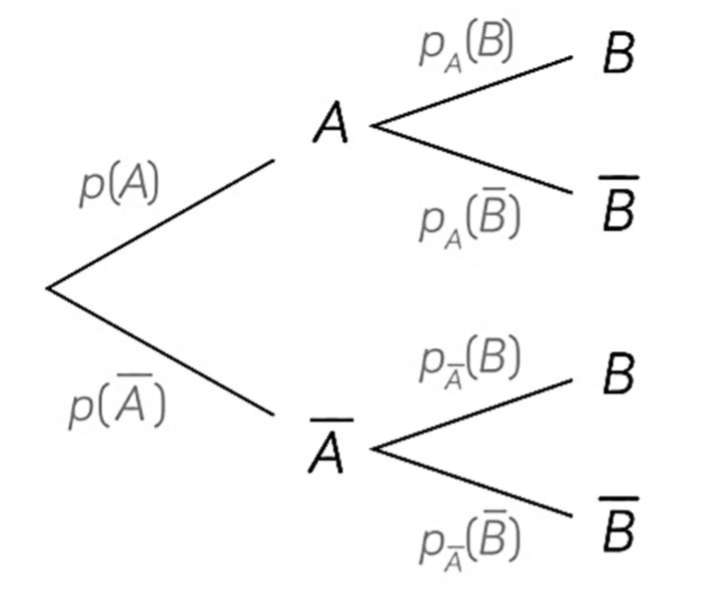
2. Utiliser un arbre pondéré pour calculer des probabilités

Propriétés :
1) Evénement contraire : La somme des probabilités inscrites sur les branches issues d’un même noeud est égale à $1$. $ P_A ( \overline{B} ) = 1 - P_A (B) $
2) Intersection d'événements : La probabilité d’un chemin est le produit des probabilités des événements inscrites sur les branches de ce chemin.
Remarque : il est possible de "renverser" l'arbre si l'on a les probabilités de $A$ sachant $B$. 		$P(A \cap B) = P(A) \times P_A (B) $
Remarque : on a aussi $ P(A \cap B) = P(B) \times P_B (A) $
Il suffit de multiplier chaque membre de l’égalité $ P_A (B) = \frac{P(A∩B)}{P(A)} $ par $ P(A)$. De même en multipliant l’égalité $ P_B (A) = \frac{P(A \cap B)}{P(B)} $ par $ P(B) $.
3) Formule des probabilités totales : La probabilité d’un événement est la somme des probabilités des chemins conduisant à cet événement.
$ P(B) = P(A \cap B) + P(A \cap \overline{B} ) $
  1. PM(F)=P(M∩F)P(M)=0,240,4=0,6.
  2. PM(F¯)=1−PM(F)=1−0,6=0,4.
    La probabilité que l’individu soit non-fumeur sachant qu’au moins un de ses parents est fumeur est de 40 %.