Maths 1EDS / G3-équations de droites

On se place dans un repère orthonormé

(O; \vec{i}, \vec{j})

.

1. Vecteur normal

Définition : Un vecteur normal à une droite $d$ est une vecteur non nul orthogonal à tout vecteur directeur de $d$ .

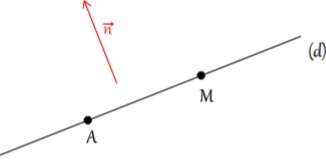
Propriété : Soit $d$ la droite passant par le point $A$ et de vecteur normal $\vec{n}$ .
Un point $M$ appartient à la droite $d$ si et seulement si les vecteurs $\vec{A M}$ et $\vec{n}$ sont orthogonaux si et seulement si $\vec{A M} . \vec{n} = 0$ .

.

2. Equation cartésienne

2.1. Théorème

Théorème :

Soit $d$ une droite de vecteur normal $\vec{n} (\begin{matrix} a \\ b \end{matrix})$ .
Une équation cartésienne de $d$ s'écrit $a x + b y + c = 0$ .

Soient $a$ , $b$ et $c$ trois nombres réels avec $(a; b) \neq (0; 0)$ .
L'équation $a x + b y + c = 0$ est celle d'une droite $d$ de vecteur normal $\vec{n} (\begin{matrix} a \\ b \end{matrix})$ .

Rappel

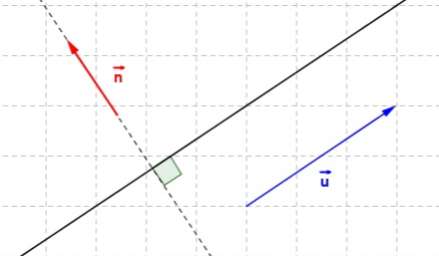
Une droite d'équation cartésienne $a x + b y + c = 0$ a pour vecteur directeur $\vec{u} (\begin{matrix} - b \\ a \end{matrix})$ .
Une droite d'équation réduite $y = m x + p$ a pour vecteur directeur $\vec{v} (\begin{matrix} 1 \\ m \end{matrix})$ .

2.2. Méthodes

2.2.1. Déterminer l'équation cartésienne d'une droite

On considère la droite $d$ passant par le point $A (3; - 1)$ et de vecteur normal $\vec{n} (\begin{matrix} - 1 \\ 5 \end{matrix})$ .
Déterminer une équation de $d$ .

méthode 1 :

$M (x; y) \in d$ ⇔ $\vec{A M} (\begin{matrix} x - 3 \\ y + 1 \end{matrix})$ et $\vec{n} (\begin{matrix} - 1 \\ 5 \end{matrix})$ sont orthogonaux.

⇔ $\vec{A M} . \vec{n} = 0$

⇔ $- 1 \times (x - 3) + 5 \times (y + 1) = 0$

⇔ $- x + 5 y + 8 = 0$

méthode 2 :

\vec{n} (\begin{matrix} - 1 \\ 5 \end{matrix})

vecteur normal à

d

donc

d

admet une équation de la forme

a x + b y + c = 0

avec

a = - 1

et

b = 5

soit

- x + 5 y + c = 0

.

A (3; - 1) \in d

donc les coordonnées de

A

vérifient l'équation de

d

.

- 3 + 5 \times (- 1) + c = 0

soit

c = 8

Conclusion : $d$ a pour équation $- x + 5 y + 8 = 0$

2.2.2. Déterminer les coordonnées d'un projeté orthogonal

On considère la droite $d$ passant par le point $A (3; - 1)$ et de vecteur normal $\vec{n} (\begin{matrix} - 1 \\ 5 \end{matrix})$ .
Déterminer les coordonnées du point $H$ , projeté orthogonal du point $B (14; - 4)$ sur la droite $d$ .

méthode : $H$ est le point d'intersection des droites $d$ et $(B H)$ .
Les droites $d$ et $(B H)$ sont orthogonales donc $\vec{u} (\begin{matrix} 5 \\ 1 \end{matrix})$ , un vecteur directeur de $d$ est un vecteur normal de $(B H)$ .

vecteur normal à

d

:

\vec{n} (\begin{matrix} - 1 \\ 5 \end{matrix})

point de

d

:

A (3; - 1)

équation de

d

:

- x + 5 y + 8 = 0

vecteur normal à

(B H)

:

\vec{u} (\begin{matrix} 5 \\ 1 \end{matrix})

point de

(B H)

:

B (14; - 4)

équation de

(B H)

:

5 x + y - 66 = 0

.

H

est le point d'intersection des droites

d

et

(B H)

donc les coordonnées de

H

vérifient le système d'équations :

${\begin{cases} - x + 5 y + 8 = 0 \\ 5 x + y - 66 = 0 \end{cases} \Leftrightarrow {\begin{cases} - 5 x + 25 y + 40 = 0 \\ 5 x + y - 66 = 0 \end{cases} \Leftrightarrow {\begin{cases} 26 y - 26 = 0 \\ 5 x + y - 66 = 0 \end{cases} \Leftrightarrow {\begin{cases} y = 1 \\ 5 x + 1 - 66 = 0 \end{cases} \Leftrightarrow {\begin{cases} y = 1 \\ x = 13 \end{cases}$

Conclusion : $H (1; 13)$ est le projeté orthogonal de $B$ sur la droite $d$ .

$\vec{u} (\begin{matrix} 5 \\ 1 \end{matrix})$ vecteur normal à $(B H)$ donc $(B H)$ admet une équation de la forme $a x + b y + c = 0$ avec $a = 5$ et $b = 1$ soit $5 x + y + c = 0$ .
$B (14; - 4) \in (B H)$ donc les coordonnées de $B$ vérifient l'équation de $(B H)$ . Ainsi $- 3 + 5 \times (- 1) + c = 0$ soit $c = 8$ .

Conclusion : $(B H)$ a pour équation $5 x + y - 66 = 0$

On multiplie les coefficients de la 1ère équation par $5$ .
On additionne le deux équations membre à membre (de cette façon, l'inconnue $x$ disparait) et on garde une des deux équations de départ.
On détermine $y$
On en déduit la valeur de $x$ avec l'autre équation.