Header
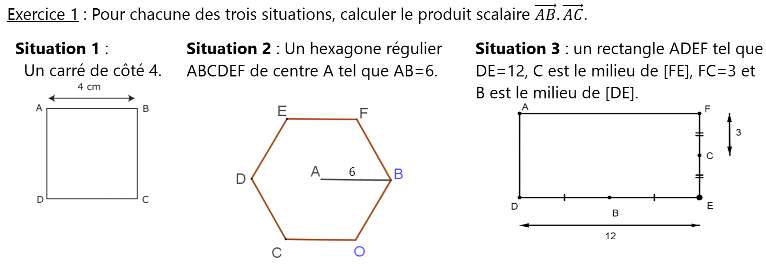
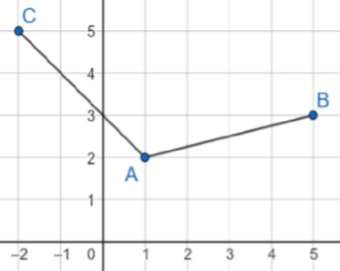
🠖 Géométrie

G2-Produit Scalaire

Cette notion est utilisée :
  • en Physique : pour mesurer l’énergie nécessaire au déplacement d’un objet soumis à une force.
    On parle du « travail d’une force ».
  • en géométrie : pour résoudre des problèmes d’angles et de distances avec des applications en cartographie par exemple.
A mémoriser :
Géométrie / G2-Produit Scalaire Apprentissage 0x Réussite 0/0
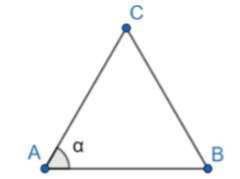
Donner la formule du produit scalaire utilisant la mesure de l'angle entre deux vecteurs $\overrightarrow{AB}$ et $\overrightarrow {AC}$.
$\overrightarrow{AB}.\overrightarrow {AC}=AB \times AC \times \cos{\widehat{BAC}}$
A savoir-faire :
  • Calcul fractionnaire
  • Résolution d'équation
  • Calcul avec les racine carrées
  • Propriétés des quadrilatères particuliers
  • Droites remarquables dans un triangle
  • Les vecteurs
  • La trigonométrie
Savoir-faire du chapitre
Exercices MathAlea

1. Définition

Soient u→(xy) et v→(x′y′) deux vecteurs dans un repère orthonormé (O;i→,j→).
Le produit scalaire de u→ et v→ est le nombre réel défini par u→.v→=xx′+yy′.
Soient $A(1;2)$, $B(5;3)$ et $C(-2;5)$ trois points dans un repère orthonormé $(O;\vec{i},\vec{j})$.
Calculer le produit scalaire $ \overrightarrow{AB}.\overrightarrow{AC}$.
$\overrightarrow{AB} \begin{pmatrix}5-1\\3-2\end{pmatrix}=\begin{pmatrix}4\\1\end{pmatrix}$ et $\overrightarrow{AC}\begin{pmatrix}-2-1\\5-2\end{pmatrix} =\begin{pmatrix}-3\\3\end{pmatrix}$
donc $ \overrightarrow{AB}.\overrightarrow{AC}=4 \times (-3) + 1 \times 3=-12+3=-9$

2. Propriétés

Pour tous vecteurs u→ , v→ , w→ et pour tous réels k on a :
  • u→.v→=v→.u→ (Symétrie du produit scalaire)
  • u→.(v→+w→)=u→.w→+v→.w→(ku→).v→=k×(u→.v→)} (Linéarité du produit scalaire)

3. Orthogonalité

3.1. Définition

On dit que deux vecteurs u⃗ et v⃗ sont orthogonaux lorsque leurs directions sont perpendiculaires.

3.2. Propriété

u→ et v→ sont orthogonaux si et seulement si 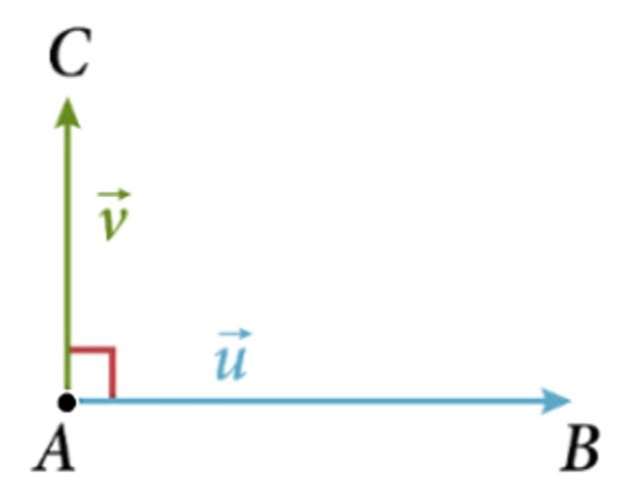u→.v→=0.
Dans l'exemple de la partie 1., les droites $(AB)$ et $(AC)$ sont-elles perpendiculaires ?

Deux droites $(AB)$ et $(AC)$ sont perpendiculaires lorsque $ \overrightarrow{AB}.\overrightarrow{AC}=0$.
or $\overrightarrow{AB}.\overrightarrow{AC}=-9 \neq 0$ donc $(AB)$ et $(AC)$ ne sont pas perpendiculaires.

4. Colinéarité

4.1. Propriété

  • Si u→ et u→ sont colinéaires et de même sens alors u→.v→=‖u→‖×‖v→‖.
  • Si u→ et u→ sont colinéaires et de sens contraire alors u→.v→=−‖u→‖×‖v→‖.

4.2. Cas particulier du carré scalaire

Propriété : u→.u→=‖u→‖2

En particulier, AB→.AB→=‖AB→‖2=AB2

Définition : on appelle carré scalaire le nombre ‖u→‖2 également noté u→2.

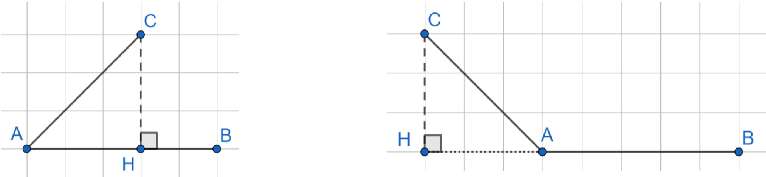
4.3. Produit scalaire et projeté orthogonal

Géométrie / G2-Produit Scalaire Apprentissage 0x Réussite 0/0/22
Quel est le projeté orthogonal du point A sur la droite (AG)

Propriété : Soit H est le projeté orthogonal de B sur la droite (OA). On a OA→.OB→=OA→.OH→

Dans chaque cas, calculer $\overrightarrow{AB}.\overrightarrow{AC}$. (Un carreau représente une unité).
$H$ est le projeté orthogonal de $C$ sur la droite $(AB)$
et $A$ est le projeté orthogonal de $A$ sur la droite $(AB)$.
On a donc $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\overrightarrow{AH}$
$\overrightarrow{AB}$ et $\overrightarrow{AH}$ sont colinéaires et de même sens
donc $\overrightarrow{AB}.\overrightarrow{AH}=AB \times AH=5 \times 3=15$
$\overrightarrow{AB}$ et $\overrightarrow{AH}$ sont colinéaires et sens contraire
donc $\overrightarrow{AB}.\overrightarrow{AH}=- (AB \times AH)=- (5 \times 3)=-15$
.

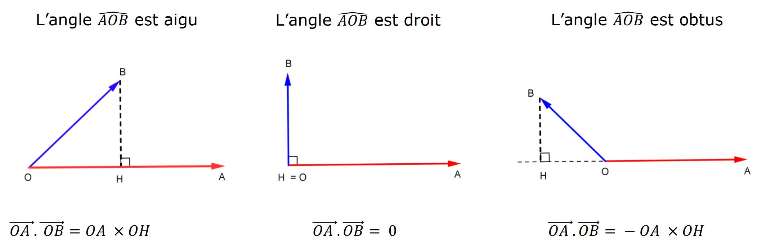
5. Produit scalaire et angle

Propriété : Soient A, B et C trois points distincts du plan.

AB→.AC→=AB×AC×cos(BAC^)

Calculer $\overrightarrow{AB}.\overrightarrow{AC}$ dans le triangle équilatéral $ABC$ de côté 7 cm.
$\overrightarrow{AB}.\overrightarrow{AC}=AB \times AC \times cos \left( \widehat{BAC} \right)=7 \times 7 \times cos \left( \frac{\pi}{3} \right)=49 \times \frac{1}{2}=24,5 $
.