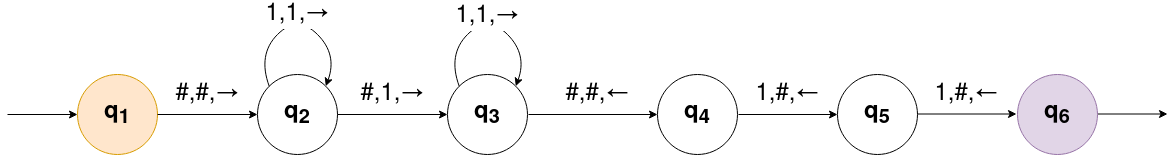Cours
Science is what we understand well enough to explain to a computer. Art is everything else we do. (D. Knuth)
Notion de programme en tant que donnée
Introduction
Un programme, stocké sur un disque dur, SSD, ou transféré sur internet lorsqu'on le télécharge, est assimilable à de l'information : ainsi, un programme est une donnée numérique.
L'Histoire retient




La thèse de Church-Turing est essentiellement une définition du caractère algorithmique, dans un sens rigoureux et général :
Un problème qui peut être résolu algorithmiquement est dit «calculable» (dans le sens : il peut être résolu par une machine de Turing).
Les machines de Turing offrent un cadre théorique qui permet de répondre (négativement) au problème de décision : «pour tout problème donné, existe-t-il un algorithme qui permet de répondre en un nombre fini d'étapes, par «oui» ou «non» à ce problème» ; on verra qu'il n'existe pas de programme qui permet de voir si un programme donné s'arrête ou boucle infiniment.

Calculabilité

Une machine de Turing est constituée d' :
- un ruban (comme le ruban magnétique d'une cassette), de longueur infinie des deux côtés, découpé en cases identiques que l'on peut lire ou sur lesquelles on peut écrire des caractères (L'alphabet peut être librement choisi. Des cases peuvent aussi rester vides et sont en général repérées par le caractère #).
- une tête de lecture qui pointe sur une case donnée ; celle-ci permet de lire et d'écrire sur la case, et peut aussi, éventuellement, se déplacer d'une case vers la gauche (symbole : ←) ou vers la droite (symbole : →).
- un «cœur» de la machine (graphe appelé automate déterministe) :
- Un ensemble fini d'états, entre lesquels on va
évoluer ; ces états peuvent être vus comme les sommets d'un graphe. On sélectionne
parmi eux :
- un état initial (la machine part de cet état, en orange sur les figures). Il est souvent repéré par une flèche entrante ;
- un ou plusieurs état(s) final(aux) (la machine effectue sa ou ses dernière(s) opération(s), puis s'arrête, lorsqu'elle arrive sur un tel état (en violet sur les figures). On parle aussi d'états acceptants, ou terminaux ; ils sont souvent repérés par une flèche sortante.
- une table d'actions (finie aussi), qui indique, en fonction
de l'état
courant de la machine et du caractère inscrit sur le ruban en face de
la tête de lecture, quel est le nouvel état, quel nouveau symbole éventuellement
inscrire sur le ruban, et quel déplacement effectuer de la tête de lecture (←, ne pas bouger ou bien →).
Cette table d'action peut être représentée par les arêtes orientées d'un graphe, chacune étiquetée par un ou plusieurs triplets : (si caractère lu, écrire caractère, déplacement éventuel). On parle de table d'action, car on peut écrire la liste d'adjacence du graphe obtenu sous forme de tableau (c'est moins lisible, cependant).
- elle est dans un état où elle ne peut rien faire pour continuer. Dans ce cas, on dit que le mot de départ sur le ruban est refusé.
- elle est entrée dans un état étiqueté comme final. Dans ce cas, on dit que le mot de départ sur le ruban est accepté.
On a représenté la machine de Turing ci-contre, dans son état initial : 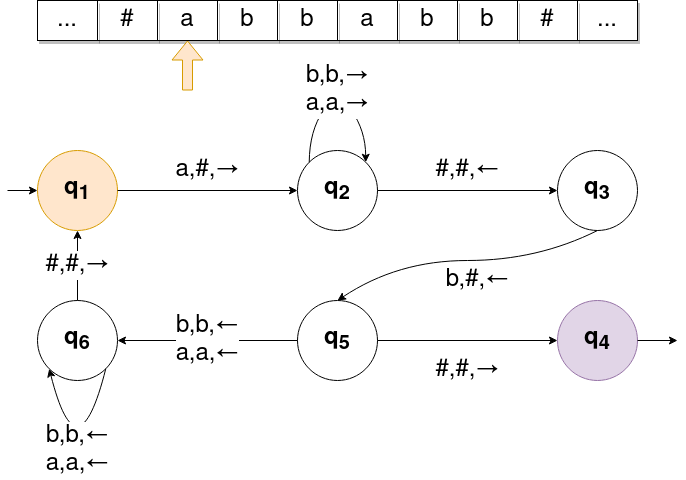
a le plus à gauche (flèche orange). Côté automate,
on part de l'état q1. Au début : on est sur
a, et une flèche sort de q1 en mentionnant
la possibilité a : on va suivre cette flèche à droite de q1, passer en
q2, et au passage, remplacer, comme mentionné par la flèche suivie, ce a
sur le ruban par un vide #, et déplacer la tête de lecture à droite.
- Le mot
abbabbest-il accepté ? - Qu'est devenu ce mot ? (état final du ruban)
- Le mot
aaabbbest-il accepté ? - Qu'est devenu ce mot ?
Pour cela, nous avons besoin de la représentation unaire des entiers. En unaire, l'entier x, noté x sera représenté par (x+1) caractères «
1» côte à côte. Ainsi : 0 sera représenté en unaire par 1 et
4 sera représenté par 11111. Pour la machine suivante, on part du mot #x̄# = #1…1# avec q1 pour état initial, et avec x un entier naturel quelconque,
écrit en unaire sur le ruban (la tête de lecture, comme précisé par la notation, pointe sur le
premier # à gauche).

- Si x = 0, que se passe-t-il ? Le mot de départ est-il accepté ou refusé ?
- Que fait cette machine pour x ≥ 1 ?
- En déduire que la fonction nulle (c'est-à-dire la fonction qui quelque soit x renvoie 0) est calculable.
- Écrire la table d'action de cette machine (sous forme de tableau).
#x̄#ȳ#, où x et y sont des entiers naturels, écrits en unaire sur le ruban avec q1 comme état initial, et
la tête de lecture pointe sur le
premier # à gauche. On pose z = x + y. Construire une machine de Turing permettant d'écrire
#z̄# ; on prouve ainsi que l'addition
des entiers est une opération calculable.
| état courant | symbole lu | symbole écrit | déplacement | état suivant |
|---|---|---|---|---|
q1 | # | 0 | → | q2 |
q2 | # | 1 | → | q1 |
Remarque : On peut coder une ou plusieurs machines de Turing à l'intérieur d'une machine de Turing : on parle de machine de Turing universelle
Cf la vidéo Science4All - La machine de Turing | Intelligence Artificielle 4
Voir la vidéo CNRS - Le modèle Turing
Décidabilité
Langage : Les problèmes peuvent être codés dans un langage formel, écrits
en utilisant un alphabet (fini) de caractères pouvant être manipulés par des machines de
Turing.
Problème de décision : C'est un problème pouvant être traité par une machine
de Turing, pour lequel on peut répondre par oui ou bien par non.
Par exemple :
- savoir si un nombre entier donné est pair ;
- savoir si un nombre entier est premier ;
- un voyageur se téléporte à chaque étape à des coordonnées GPS différentes. Est-il apparu à Toulouse avant la 100ème téléportation ?
- un voyageur se téléporte à chaque étape à des coordonnées GPS différentes. Est-il apparu à Toulouse à une étape donnée ?
Décidabilité : On dit qu'un problème est décidable lorsqu'il
est calculable et qu'une machine de Turing permet de répondre "oui" par un état
final ou bien "non" par un arrêt sur un autre état, c'est-à-dire répondre au problème
en un nombre fini d'étapes. Concrètement, il existe un algorithme qui permet de répondre au problème et il s'arrête
en donnant la réponse.
Dans le cas contraire, on dit que le problème est indécidable.
S'il existe un algorithme pouvant répondant "oui" en un nombre fini d'étapes, mais ne pouvant
pas répondre "non" en un nombre fini d´étapes, on dit que le problème est semi-décidable.
Problème de l'arrêt : Ce problème cherche à savoir s'il existe un programme
(appelons-le halt()), qui prend en entrée n'importe quel programme x (donné
sous forme de chaîne de caractères, ou bien codé sous forme de nombre, par exemple)
et précise si x s'arrête ou non.
Trop beau pour être vrai ! On va voir que ce problème est indécidable, et qu'un tel programme
halt ne peut exister.
Examinons l'algorithme suivant :
TURING(n) # n est un entier naturel
1. LISTER (sans les exécuter) tous les programmes de taille inférieure ou égale à n caractères,
qui prennent un entier en entrée et renvoient un entier en sortie.
# c'est long, mais possible par reconnaissance de la syntaxe et de la grammaire
# de ces programmes ; aussi, ces programmes sont en nombre fini.
2. SÉLECTIONNER parmi cette liste ceux qui s'arrêtent avec halt() lorsque leur entrée est n.
3. EXÉCUTER chacun des programmes sélectionnés et choisir le plus grand des entiers Smax
apparu en sortie de ces programmes.
4. RETOURNER Smax + 1.n0 sa taille en caractères.Notons que 1., 2. ,3. et 4., par construction, contiennent uniquement des étapes qui s' arrêtent : globalement, le programme
TURING() s'arrête.Exécutons
TURING(n0) :
TURING(n0)se liste lui-même puisque sa taille est inférieure ou égale àn0.- l'entrée de
TURING()étantn0, et celui-ci s'arrêtant par construction, il est sélectionné parhalt. TURING(n0)renvoie un entier qui est forcément inférieur ou égal àSmax...- ... alors qu'il devrait renvoyer
Smax + 1... CONTRADICTION !
halt ne peut donc pas exister : sinon, on pourrait s'en servir pour
écrire un programme qui renvoie une sortie plus grande que la sortie qu'il renvoie. Paradigmes en informatique
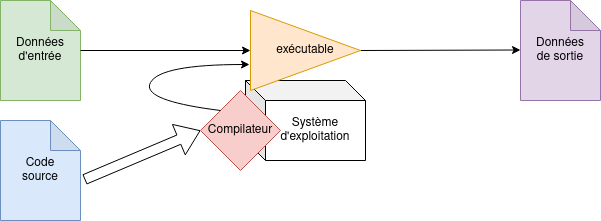
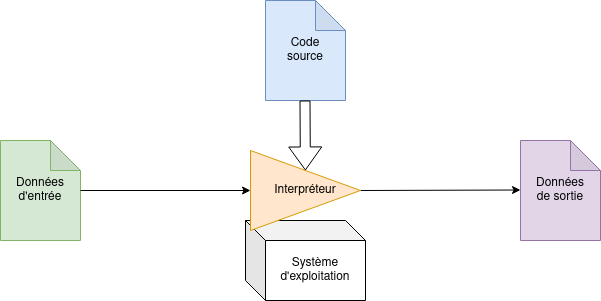
Langages interprétés ou compilés
Pour exécuter un programme, on peut, encore aujourd'hui, produire un exécutable à partir
d'un script où sont écrites, à l'aide d'une syntaxe minimale, une suite d'
instructions (hardware) du processeur permettant d'agir directement sur les registres.
On appelle ce pseudo-langage l'assembleur ; il est propre à
chaque processeur car leurs
jeux d'instructions peuvent être différents. On le qualifie de langage de bas niveau, dans
le sens où il est très proche du matériel ; le plus proche étant le langage
machine, qui
est essentiellement de l'assembleur écrit en binaire. Voici un exemple d'opération écrite
en assembleur (ces instructions sont assez communes et ce script marcherait sur bon
nombre de processeurs) :
;pour calculer (7+6)%3, on aura le code suivant :
MOV AX, 7 ; Le registre AX reçoit la valeur 7.
ADD AX, 6 ; On ajoute à AX la valeur 6, le résultat est stocké dans la destination, soit AX.
MOV BX, 3 ; On met dans le registre BX la valeur 3 qui servira de source à la division.
DIV BX ; On divise AX par la source, ici BX, qui vaut 3
;le résultat de la division est stocké dans la destination (BX)
;et le modulo (reste de la division qui nous intéresse ici) est mis dans DXCf Wikiversity

Python, C, C++, C#, Arduino, Bash,Javascript, HTML+CSS, SQL, Haskell.

Avec Java, le code source est compilé en un fichier
.jar (bytecode) qui sera exécuté par la
machine virtuelle Java adaptée au système d'exploitation sur lequel
on exécute le programme. Les .jar sont donc portables sur tous les systèmes disposant
d'une machine virtuelle du même type. Cette grande portabilité est une des raisons
qui a poussé les concepteurs d'Android à baser leur système d'exploitation sur Java. - Si on se rapproche du matériel (code assembleur), on dit que le langage est de bas niveau ;
- Si on se rapproche d'un langage de type humain (en ajoutant des fonctionalités, ...), on dit que le langage est de haut niveau.

Paradigmes de programmation
- vision du monde : modéliser une situation pour la transformer en programme ;
- méthode de travail : la présentation formelle qui va traduire cette vision.
Nous avons déjà étudié la programmation impérative (et ses réalisations itératives et récursives) ainsi que la programmation orientée objet en début d' année.
Nous utilisons aussi parfois, en Python, le paradigme fonctionnel. Le principe est de composer (enchaîner) des fonctions. En ayant des fonctions rigoureusement spécifiées, on limite, voir on élimine les effets de bord, et donc bon nombre d'erreurs possibles, tout en rendant le code source concis et lisible.
Haskell est un bon exemple de langage de programmation fonctionnelle. Liens pour découvrir ce langage : nokomprendo et univ-lille1.fr.

Attention, l'idée du paradigme fonctionnel n'est pas seulement d'utiliser des fonctions mais d'utiliser des fonctions dites pures. Il s'agit de fonctions qui ne modifient pas l'état courant des variables. Autrement dit, le résultat renvoyé par une fonction pure ne doit dépendre que de valeurs passées en paramètres et pas de valeurs externes à la fonction. De plus une fonction pure ne doit pas modifier les valeurs des variables externes, globales.
- La fonction suivante est-elle une fonction pure ? Sinon, modifier cette fonction pour la rendre pure.
def est_majeur(age): return age >= 18 - La fonction suivante est-elle une fonction pure ? Sinon, modifier cette fonction pour la rendre pure.
liste = [1, 6, 4] def ajouter(x): liste.append(x) return liste -
Attention, la fonction suivante n'est pas pure !
def ajouter(liste, x): # Cette fonction n'est pas pure liste.append(x) return liste
Avec un même langage de programmation, on peut utiliser des paradigmes différents.
Dans un même programme, on peut utiliser des paradigmes différents.
- selon le paradigme de programmation impératif (instructions simples sans fonction, ni objet).
- selon le paradigme de programmation procédural (définition d'une procédure sous forme de fonction ou de module).
- selon le paradigme de programmation fonctionnel (aucune création, ni modification de variable).
- selon le paradigme de programmation orienté objet (utilisation d'un constructeur d'objet).
Mise au point des programmes
Cette partie est la suite logique du chapitre sur les spécifications et les tests vu en première NSI.
Rappels sur les assertions
assert condition
assert condition, "message d'erreur"L'assertion vérifie qu'une condition est respectée, sinon elle stoppe l'exécution du programme et
peut afficher un message d'erreur (celui-ci est facultatif).
Une assertion permet de stopper préventivement une exécution avant qu'une erreur ne se produise. Elles
sont des outils de développement et ne doivent pas apparaître dans un programme final, livrable. En supprimant toutes les
assertions d'un script, le programme doit continuer à fonctionner normalement.
Le mode de programmation qui utilise des assertions est appelée programmation défensive. Elle suppose que les fonctions sont correctement utilisées,
mais prévoit des garde-fous : les assertions, qui permettent de vérifier les préconditions et les postconditions et ainsi de détecter des bugs
au cours du développement.
Ce type de programmation est utilisé pour du code dont on a le contrôle. Par exemple lorsqu'on écrit un module, pour les fonctions qui sont destinées à n'être appelées que dans ce module. Pour les fonctions destinées à être appelées par d'autres modules/scripts/personnes, il est préférable de faire une gestion active des erreurs avec une structure conditionnelle qui retourne des valeurs facilement interprétables et si possible de même type que autres retours.
-1, à l'aide d'une structure conditionnelle.
def indice(liste, element):
"""Renvoie l'indice de la première occurence de l'élément dans la liste."""
assert element in liste, "L'élément doit être dans la liste."
return liste.index(element)
print(indice(["a", "b", "c", "d"], "e"))Modularité
Définition
La modularité est le fait de décomposer un programme en plusieurs fonctions/modules/fichiers.
La modularité présente des avantages d'autant plus fort qu'un projet est important :
- Le découpage en sous-parties indépendantes permet la réutilisation du code pour d'autres projets.
- La structuration d'un projet en plusieurs sous-projets, rend le projet inital plus réalisable, compréhensible et maintenable.
- La modularité est une nécessité pour l'organisation d'un projet et le partage des tâches au sein d'une équipe.
Cette modularité existe à plusieurs échelles :
- Dans un programme d'une centaine de lignes regroupées dans un seul fichier, elle apparaît sous la forme d'importation de modules/bibliothèques en début de script ou bien dans la conception de fonctions réutilisables.
- Pour un programme d'un millier de lignes, l'intérêt de le découper en plusieurs fichiers apparaît pour en facilité l'écriture et la maintenance, pour isoler une classe d'objet particulière ou un ensemble de fonctions placées dans un fichier auxiliaire ou pour séparer une interface graphique du coeur du programme dans deux fichiers distincts.
- Pour un projet plus conséquent de 10 000 lignes, la modularité permet d'organiser le code, de permettre le développement en parallèle de plusieurs parties.
Un module constitue une "brique" logicielle d'un projet, pouvant éventuellement être utilisé par d'autres projets. Il est donc important de s'assurer de son indépendance vis-à-vis du reste du projet et de la cohérence des missions qu'il assure. De plus, il est important de le documenter convenablement afin de le rendre compréhensible et facilement réutilisable.
Avec Python
Il existe un grand nombre de modules natifs au moteur Python. La liste exhaustive est disponible dans la Doc Python en ligne. Parmi eux, en voici quelques-uns particulièrement utilisés :
| Module | description |
|---|---|
tkinter | interface graphique |
math | fonction et constantes mathématiques |
random | génération de nombres aléatoires |
statistics | fonctions de mathématiques statistiques |
time | fonctions liées au temps |
os | interaction avec le système d'exploitation, gestion des fichiers |
smtplib | interaction avec un serveur SMTP |
turtle | affichage graphique |
sqlite3 | interaction avec une BD |
pip | gestion et installation de modules supplémentaires |
PIL | traitement d'image |
NumPy | calcul numérique et matriciel |
Matplotlib | tracé graphique |
Il en existe beaucoup d'autres, développés par la grande communauté des développeurs Python et qui nécessiteront une installation supplémentaire. Ils sont en général accompagnés d'un site internet les documentant
En python, les modules sont importés grâce au mot clé import proposant plusieurs syntaxes :
from math import *
print(pi)from math import pi
print(pi)import math
print(math.pi)import math as m
print(m.pi)Attention, la première syntaxe importe directement dans l'espace des noms du programme, tout ce que contient le module (*).
Cela peut entraîner une surcharge de nom, c'est-à-dire l'écrasement d'une variable ou d'une fonction par une autre varible ou une autre fonction portant le même nom.
Ce risque de surcharge est facilement évitable à l'aide des autres syntaxes. En n'important qu'une fonction du module (syntaxe 2)
ou en nommant explicitement le module (syntaxe 3) ou en le renommant (syntaxe 4) lors de l'utilisation d'une de ses fonctions.
Pour créer vos propres modules, il suffit de créer un fichier python mon_module.py à la racine de votre projet et de
l'importer avec les mêmes syntaxes proposées par l'instruction import.
from mon_module import *
from mon_module import ma_fonction
import mon_module
import mon_module as mmPour un site internet
Dans le cas d'un site internet, la modularité est déjà prise en compte dans le découpage fonctionnel des fichiers HTML, CSS et JS. Pour rappel, les fichiers HTML hébergeant le contenu du site, les fichiers CSS, sa mise en page et les fichiers JS assurant son interactivité.
Comme pour la plupart des langages de programmation, la modularité est également permise en javascript.
Par exemple sur ce site de cours de NSI, la mise en page des codes est sous-traitée à un module
(fichier javascript) intitulé prism.js utilisant également un fichier CSS prism.css. Ces deux
fichiers ont été téléchargés depuis le site prismjs.com et intégrés
aux fichiers du site.
De la même façon qu'en python, les modules sont importés en début de script, nous trouverons dans la balise <head> d'une page HTML, des liens vers des fichiers Javascript. Ces fichiers peuvent tout aussi bien être locaux (repéré par leur chemin relatif) ou bien hébergé
ailleurs sur internet (repéré par leur URL).
<head>
<meta charset="utf-8" />
<title>C9-Programmation</title>
<link rel="stylesheet" type="text/css" href="styles/style.css" />
<link rel="stylesheet" type="text/css" media="print" href="styles/print.css"/>
<link href="styles/prism.css" rel="stylesheet" />
<script src="scripts/interactif.js" defer></script>
<script src="scripts/prism.js" defer></script>
<script async="true" src="https://cdn.jsdelivr.net/npm/mathjax@2/MathJax.js?config=AM_CHTML" defer></script>
</head>Gestion des bugs
En programmation, savoir répondre aux causes de bugs et tester ses scripts est essentiel pour obtenir un programme fiable et robuste.
3.3.1. Environnement de Développement Intégré
Un bon Environnement de Développement Intégré (EDI) fournit plusieurs outils permettant de limiter l'apparition de bugs. Il doit permettre :
- la complétion intelligente du code pour éviter les erreurs de frappe,
- l'inspection du code avec la mise en évidence d'erreurs et leur correction rapide,
- la refactorisation du code et une navigation riche pour en faciliter la relecture,
- l'exécution en mode debug, c'est-à-dire pas à pas avec affichage de l'état courant des variables, afin de diagnostiquer un bug.
Conçu pour le langage python, la version PyCharm Community
est un EDI libre, gratuit et assez ergonomique qui propose ces fonctionnalités.
Vous pouvez les retrouver également dans Visual Studio Code qui est un
EDI généraliste (plusieurs langages) et qui propose de nombreuses extensions très intéressantes.
Liste non-exhaustive de conseils pour éviter les bugs
- Corriger tout de suite les bugs évidents, mis en relief par votre EDI.
- Prévoir toutes les saisies possibles d'un utilisateur et imaginer le pire pour rendre votre code robuste.
- Créer et appliquer des jeux de tests (avec des assertions par exemple) vérifiant tous les cas d'utilisation de votre code :
- les cas limites (le zéro, une chaîne de caractère vide ou une liste vide, le premier ou le dernier élément d'une séquence ...).
- tous les cas d'une structure conditionnelle.
- En python, il faudra faire bien attention à l'indentation. Un programme mal indenté peut donner une réponse éronnée sans lever d'erreur.
- Éviter les effets de bord qui sont sources de nombreuses erreurs. Pour cela il faut éviter d'utiliser des variables globales et des fonctions qui modifient des variables externes. Utiliser une dose de programmation fonctionnelle.
- Éviter les comparaisons entre flottants.
- Donner des noms intelligibles à vos variables, vos fonctions, vos classes ...
- Dans le cas des boucles non-bornées
while:- s'assurer que l'on puisse entrer dans la boucle (condition vraie).
- s'assurer que la condition puisse devenir fausse, on parle alors de condition d'arrêt, afin d'éviter les boucles infinies. Pour cela, le variant de boucle doit évoluer à chaque itération de la boucle vers la condition d'arrêt.
- Dans le cas des boucles bornées
for, il faudra éviter pendant l'exécution de la boucle de modifier la liste que l'on est en train de parcourir. - Tester vos scripts (fonctions, modules) en cours de développement avec des assertions.
- Appliquer une batterie de test avant de livrer votre code.
a = 0.0
while a != 0.3:
a += 0.1
print(a)
print("C'est fini !")def supprimer_les_nombres_pairs(liste):
for i in range(len(liste)):
if liste[i]%2 == 0:
liste.pop(i)
return liste
liste = [i for i in range(10)]
print(supprimer_les_nombres_pairs(liste))Les exceptions en python
Quand le moteur Python rencontre une erreur, il lève une exception.
Une exception est un objet en python qui est définie par son type.
Voici une liste non exhaustive de types d'exception :
| Type d'erreur | Description |
|---|---|
SyntaxError |
Le code ne peut pas être exécuté car l'analyseur a repéré une erreur dans la syntaxe de python. Il peut s'agir de deux-point ":" manquant, de parenthèses mal couplées ou d'indentation manquante. L'analyseur qui ne reconnaît plus la syntaxe de python, signale une ligne d'erreur mais attention la faute de syntaxe est souvent localisée avant cette ligne. |
ZeroDivisionError |
Erreur de division par zéro. |
NameError |
Une variable, une fonction, une classe, invoquée ... n'est pas précédement définie. |
TypeError |
L'opérateur n'accepte pas le type d'opérande qui lui est donné. |
ValueError |
Ici l'opérateur reçoit le bon type d'opérande mais sa valeur est inappropriée. |
IOError |
Le fichier n'existe pas. |
RecursionError |
La limite de la pile d'appels récursifs a été atteinte. Elle est de 1000 par défaut et peut être modifiée. |
IndexError |
L'indice pour une séquence, ou la clé pour un dictionnaire n'existe pas. |
AssertionError |
Une assertion est fausse. |
KeyboardInterrupt |
L'exécution est stoppée par l'utilisateur (fermeture de fenêtre par exemple). Contrairement aux autres erreurs,
il ne s'agit pas d'un objet Exception, en python. Par exemple,
il ne sera pas capter par l'instruction except Exception :, contrairement à toutes les autres.
Par contre, il sera capter par l'instruction except :.
|
x = int(input("Entrez un nombre : "))age = input("Entrez votre age : ")
if age >= 18:
print("Vous êtes majeur.")Gestion des exceptions en python
Python propose une syntaxe afin de gérer les erreurs.
try:
# instructions à exécuter
except """type d'erreur 1""" :
# instructions à exécuter si ce type d'erreur est levée
except """type d'erreur 2""" : # Un deuxième except est facultatif
# instructions à exécuter si ce type d'erreur est levée
else: # Factultatif
# instructions à exécuter s'il n'y a pas eu d'erreur
finally: # Facultatif
# instructions à exécuter dans tous les cas même si un return existe dans un bloc exceptRemarque : Il est possible de ne pas préciser le type d'erreur à attraper
après except:, mais cela est déconseillé
car toutes les erreurs levées ne se valent pas et cela peut être source d'erreurs supplémentaires
en capturant une erreur qui n'aurait pas dû l'être et qui sera alors invisible.
try: except: else:
afin qu'aucune erreur ne soit levée quelque soit l'action de l'utilisateur et qu'il soit informé de son éventuelle erreur.
age = int(input("Entrez votre age : "))
if age >= 18:
print("Vous êtes majeur.")
else:
print("Vous êtes mineur.")Il est également possible de lever soi-même une erreur à l'aide du mot clé raise ou
bien encore de récupérer une erreur dans une variable.
- Tester l'instruction :
raise NameError("Ce nom de variable n'existe pas."). - Compléter/modifier le script suivant en levant les bonnes exceptions
et en les capturant pour afficher un message clair à l'utilisateur.
def majeur(age): if type(age) != type(1): raise # à compléter if age < 0: raise # à compléter if age >= 18: return "majeur" return "mineur" age = -1 try: print("Vous êtes {0}.".format(majeur(age))) except TypeError as er: print("Erreur :", er) except ValueError as er: print("Erreur :", er)
L'utilisation des assertions dans une structure de gestion des erreurs permet de personnaliser encore davantage les messages d'erreur.
age = input("Entrez votre âge :")
try:
age = int(age)
assert age >= 0, "Vous ne pouvez pas avoir un âge négatif."
assert age < 200, "Vous ne pouvez pas avoir plus de 199 ans."
except ValueError:
print("Vous devez entrer uniquement des caractères numériques.")
except AssertionError as msg :
print(msg)Le typage des variables
En apparence, python ne se soucie pas des types de variable : lorsqu'on initialise une variable, à aucun moment on ne doit déclarer son type et à tout moment, on peut écraser le contenu d'une variable par une valeur d'un autre type. C'est assez pratique car cela allège le code mais au risque de générer des erreurs.
>>> a = "Hello, World"
>>> print(type(a))
<class str>
>>> a = 3 + 2
>>> print(type(a))
<class int>
Cet exemple montre que Python connaît bien le type de ses variables et qu'il vous autorise à en changer comme bon vous semble. Le risque est d'affecter de mauvaises valeurs à une variable sans s'en rendre compte et ainsi génerer des bugs. Certains langages comme le C obligent à déclarer au préalable les variables et leurs types. Le compilateur va alors détecter les erreurs de typage et avertir le développeur des problèmes avant même qu'ils ne se produisent mais ce n'est pas le cas en python.
Il est possible de réaliser à partir de python 3.10 des annotations de type, qui sont utiles pour le développeur. L'Environnement de Développement Intégré pourra les exploiter pour avertir en cas d'erreurs ou faire des suggestions pertinentes limitant le risque d'erreurs.
Exemple : Ces deux fonctions sont fonctionnellement équivalentes mais la seconde comporte des informations de type utilisé par l'EDI pour aider le développeur.
def triple(x):
return 3 * x
def triple_v2(x: int) -> int:
return 3 * x3.4. Gestion du code avec git
Le contrôle de versions permet de suivre les modifications, faites par qui et pourquoi, ce qui devient crucial pour de gros projets et le travail d'équipe.
Voir la Documentation de Git
3.5. Zen
Exécuter la ligne de commande
import this dans la console python pour re-découvrir les
grands principes de python : The Zen of Python (PEP 20)
3.6. Bibliographie
- Olivier Lecluse - Site - Mise au point des programmes - gestion des bugs
- Cédric GERLAND - Youtube - 1ère et Terminale NSI - Mise au point de programmes et gestion des bugs en Python
- David Roche - Site - Pixees NSI Terminale
- Livre - Spécialité Numérique et sciences informatiques Terminale Compétences attendues - Editions Ellipses 2019
- Livre - Spécialité Numérique et sciences informatiques Terminale 24 leçons avec exercices corrigés - Editions Ellipses 2019
- Livre - Interros des Lycées, Numérique et Sciences Informatiques (NSI) 1re - Les vrais exos - Editions Nathan 2019