Introduction : les structures de données
- les listes, piles ou files qui sont des structures linéaires
- les dictionnaires où elles sont associées par paire
{clé: valeur} - les tables ou tableaux
- les arbres qui permettent de hiérarchiser les données et qui sont l'objet de ce chapitre
- et les graphes où les données sont en réseau (structure relationnelle) qui seront traités dans le chapitre suivant.
Les arbres
Introduction
- le découpage d'un livre en chapitres, sections, paragraphes ...
- l'arborescence d'un système de fichier
- les formats de fichier XML (par balisage) tel que le HTML
- l'organigramme d'une organisation
- la recherche dichotomique
- la compression de données (code Huffman)
- les expressions arithmétiques
- les tris, notamment ceux utilisant la stratégie "diviser pour régner"
Définition
- une racine (premier noeud)
- des noeuds (ou sommets)
- des branches (ou arêtes)
- des feuilles (noeud sans fils)
Les noeuds qui ne sont pas des feuilles sont aussi qualifiés de noeuds internes.
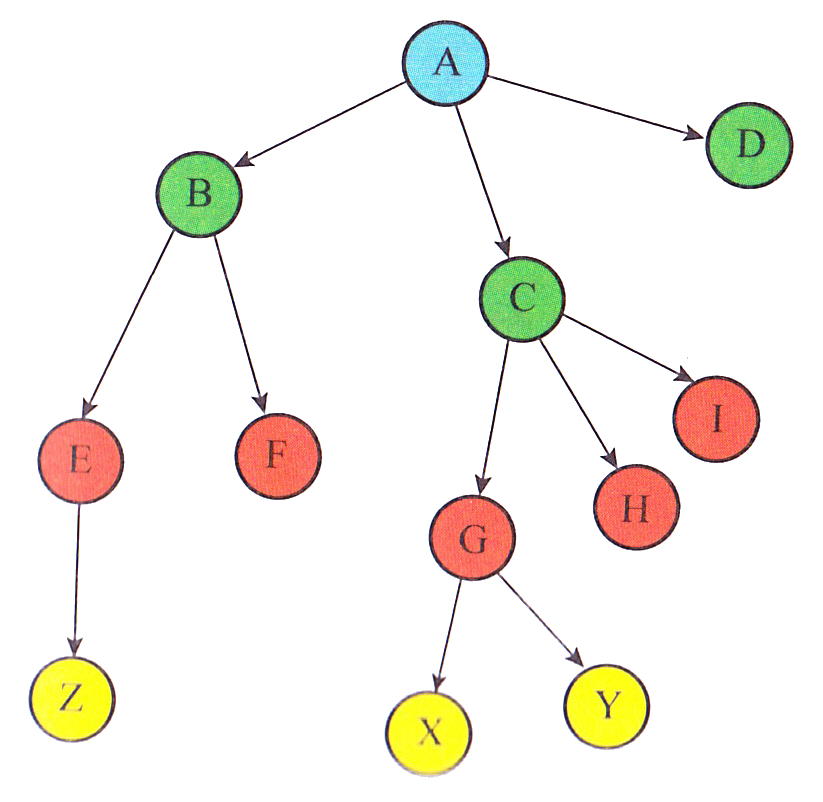
Exemple d'arbre ayant 7 noeuds, 4 feuilles, 6 branches et pour racine : le noeud A.

- le noeud B a deux fils : les noeuds E et F.
- le père du noeud B est le noeud A.
- les noeuds E et F sont frères.

Caractéristiques
- son arité qui est le nombre maximum d'enfant que peut avoir un noeud,
- sa taille qui est le nombre de noeud qu'il possède,
- sa hauteur (ou sa profondeur) qui est le nombre de branches
entre la racine et la feuille la plus éloignée.
On parle aussi de niveau : Un arbre de hauteur 3 possède 4 niveaux.
On peut faire l'analogie pour un immeuble de 4 niveaux soit un rez-de-chaussée et 3 étages (hauteur 3).
Ainsi un arbre consitué d'un seul noeud (sa racine) aurait une hauteur de 0 et 1 seul niveau.
Attention : La convention choisie dans les épreuves du baccalauréat confond hauteur et niveau, ainsi un arbre constitué d'un seul noeud (sa racine) est de hauteur 1 et possède 1 seul niveau.
Question focus (Restez dans le cadre !)

Exemple : Le HTML

Les arbres binaires
Vocabulaire
- Un arbre binaire est un arbre d'arité 2. Cela signifie que la racine et chaque noeud ne peut avoir au maximum que deux enfants. On parlera alors de sous-arbre gauche (noté SAG) et de sous-arbre droit (noté SAD). Le fils gauche est la racine du SAG tandis que le fils droit est la racine du SAD.
- Un arbre dégénéré est filiforme. Chaque noeud n'a qu'un enfant.
- Un arbre binaire localement complet est un arbre dont chaque noeud a strictement deux enfants.
- Un arbre binaire complet est un arbre localement complet avec toutes ses feuilles à la même profondeur. On dit aussi qu'il est parfaitement équilibré.
Exemple : Expressions arithmétiques
Les expressions arithmétiques sont représentables sous forme d'arbre binaire. En effet les opérateurs d'addition, de soustraction, de multiplication ou de division sont d'arité 2, c'est-à-dire qu'ils s'appliquent à deux opérandes. Les arbres binaires, par définition d'arité 2, sont donc tout désignés pour les repésenter.

Représentation d'un arbre binaire
Sous forme d'une liste
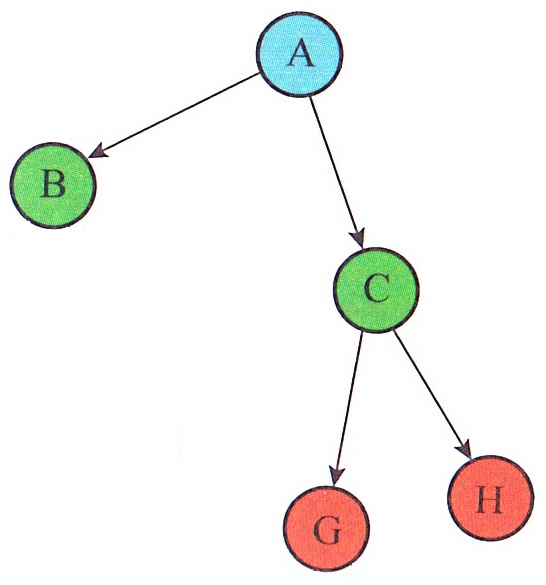
L = [A, B, C, , , G, H]Les espaces vides dans la liste correspondent aux noeuds vides dans l'arbre binaire complet correspondant. Cette représentation repose sur la relation suivante entre les indices d'un père et de ses fils :
Sous forme de listes imbriquées
Pour l'Arbre 03, rappelé ci-dessous, on peut aussi imaginer cette structure :
L = [A, B, [C, G, H]]
Sous forme d'un dictionnaire
Reprenons toujours l'exemple de l'Arbre 03. Sa représentation sous forme de dictionnaire peut être :
D = {racine:A, sag:B, sad:{racine:C, sag:G, sad:H}}Ici, chaque arbre et sous-arbre est un dictionnaire avec trois clés : la racine, le SAG et le SAD.

4.4. Implémentation en POO
class Noeud :
def __init__(self, valeur) :
self.valeur = valeur
self.gauche = None
self.droit = None
a = Noeud("A")
a.gauche = Noeud("B")
a.droit = Noeud("C")_
en préfixe de leur nom. Ils sont directement modifiables par l'utilisateur. TAD Arbre Binaire
- creerArbre(arbre, racine) → arbre
- estVide(arbre) → booléen
- nombreFils(arbre) → entier
- racine(arbre) → valeur
- sag(arbre) → arbre
- sad(arbre) → arbre
- assembler(arbre, arbre, arbre) → arbre
class Arbre:
"""Implémentation de la structure de données «Arbre» en Python."""
# creerArbre(arbre, racine) → arbre
def __init__(self, racine=None):
self._racine = racine # valeur
self._gauche = None # Sous-arbre gauche
self._droit = None # Sous-arbre droit
# estVide(arbre) → booléen
def estVide(self):
return self._racine is None
# racine(arbre) → valeur
def racine(self):
assert not self.estVide(), "L'arbre est vide."
return self._racine
# sag(arbre) → arbre
def sag(self):
return self._gauche
# sad(arbre) → arbre
def sad(self):
return self._droit
# assembler(arbre, arbre, arbre) → arbre
def assembler(self, sag = None, sad = None):
assert not self.estVide(), "L'arbre est vide."
self._gauche = sag
self._droit = sad
# définition de l'impression (print) de l'objet
def __str__(self):
return "({},{},{})".format(self._racine, self._gauche, self._droit)
# définition de l'affichage d'appel de l'objet
def __repr__(self):
return "Arbre()"
# affiche l'arbre binaire dans la console
def afficher(self):
if self.estVide():
print("L'arbre est vide.")
else:
self._afficher(0)
def _afficher(self, level):
if self._droit:
self._droit._afficher(level + 1)
print("{}{}".format(' ' * 4 * level, self._racine))
if self._gauche:
self._gauche._afficher(level + 1)-
Les attributs
_racine_gauche_droit_ -
Python ne permet pas de rendre réellement privé un attribut ou une
méthode, comme c'est le cas en C ou en Java. L'underscore
_ -
Des méthodes d'affichage
__str__()__repr__()afficher()
- Récupérer le fichier TAD_Arbre.py.
- Créer une instance pour cet arbre grâce à la classe fournie.
- S'approprier l'objet en utilisant toutes ses méthodes.
Algorithmes sur les arbres binaires
Parcours en largeur d'un arbre binaire

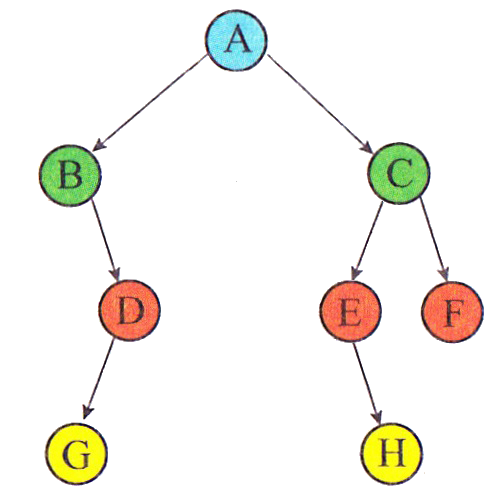
Le parcours en largeur d'un arbre binaire consiste à parcourir l'arbre,
niveau par niveau en partant de la racine en en lisant les noeuds de
gauche à droite.
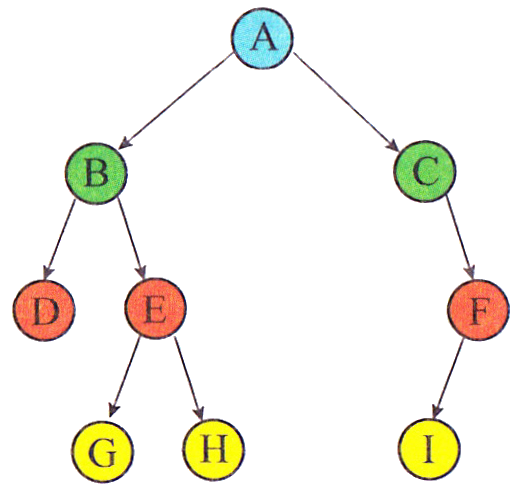
Le parcours en largeur de l'arbre ci-dessus donne : A-B-C-D-E-F-G-H-I
Pseudo code : L'algorithme de parcours en largeur utilise une file.
f ← file vide
p ← liste vide
Enfiler l'arbre dans f
TANT QUE f n'est pas vide FAIRE
arbre ← défiler f
ajouter la racine de arbre dans p
SI arbre a un fils gauche FAIRE
enfiler le sous-arbre gauche dans f
SI arbre a un fils droit FAIRE
enfiler le sous-arbre droit dans f
RETOURNER p- Récupérer le fichier TAD_File.py.
- Importer le module dans le fichier
TAD_Arbre.pyen ajoutant dans les premières lignes l'instruction :from TAD_File import *. - Compléter la méthode
parcoursLargeur(self)en y implémentant l'algorithme ci-dessus.
Parcours en profondeur d'un arbre binaire
Lors du parcours en profondeur d'un arbre, nous passons sur chaque noeud à trois reprises, avant son fils gauche, entre ses deux fils et après son fils droit.
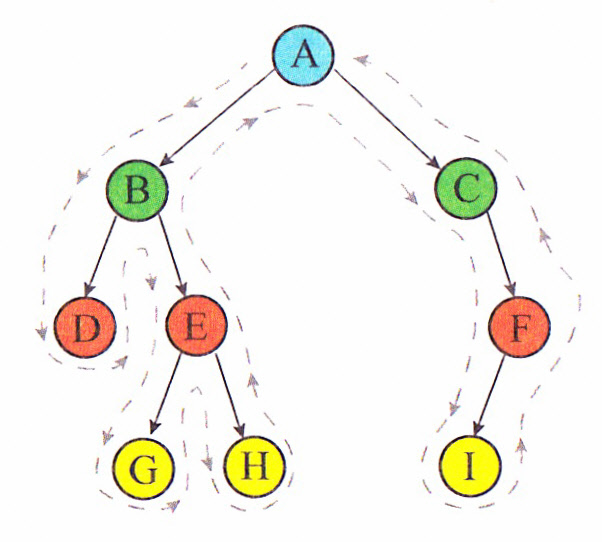
(Image cliquable)
-
Lorsqu'on traite un noeud dès sa première visite (ronds rouges en cliquant sur l'image), nous obtenons l'ordre du parcours en profondeur préfixe des noeuds. Algorithmiquement, cela revient à faire :
[racine] + appel récursif sur SAG + appel récursif sur SAD
Le parcours en profondeur préfixe de l'arbre binaire 01 ci-contre donne : A-B-D-E-G-H-C-F-I -
Lorsqu'on traite un noeud lors de sa deuxième visite (carrés bleus), nous obtenons l'ordre du parcours en profondeur infixe des noeud. Algorithmiquement, cela revient à faire :
appel récursif sur SAG + [racine] + appel récursif sur SAD
Le parcours en profondeur préfixe de l'arbre binaire 01 ci-contre donne : D-B-G-E-H-A-C-I-F -
Lorsqu'on traite un noeud lors de sa troisième visite (triangles verts), nous obtenons l'ordre du parcours en profondeur postfixe des noeud. Algorithmiquement, cela revient à faire :
appel récursif sur SAG + appel récursif sur SAD + [racine]
Le parcours en profondeur postfixe de l'arbre binaire 01 ci- donne : D-G-H-E-B-I-F-C-A
Question focus (Restez dans le cadre !)

- Compléter la méthode
_parcoursPre(self, liste)de la classeArbre(), qui retournent la liste des noeuds obtenue selon un parcours en profondeur préfixe. - Compléter la méthode
_parcoursInf(self, liste)de la classeArbre(), qui retournent la liste des noeuds obtenue selon un parcours en profondeur infixe. - Compléter la méthode
_parcoursPost(self, liste)de la classeArbre(), qui retournent la liste des noeuds obtenue selon un parcours en profondeur postfixe.
Taille d'un arbre binaire
- 𝑇(A) = 0 si A est un arbre vide
- sinon 𝑇(A) = 1 + 𝑇(sag(A)) + 𝑇(sad(A))
Pseudo code : Algorithme pour déterminer la taille d'un arbre.
a ← arbreBinaire
FONCTION taille(a):
SI a EST vide:
RETOURNER 0
SINON:
t ← 1
SI a A sag:
t ← t + taille(sag)
SI a A sad:
t ← t + taille(sad)
RETOURNER ttaille(self) dans la définition de la classe Arbre() en y implémentant l'algorithme ci-dessus.
Hauteur d'un noeud
La hauteur (ou la profondeur) d'un noeud est le nombre de branches entre ce noeud et la racine de l'arbre. La hauteur d'un noeud est définit par :
- 𝐻(x) = 0 si x est la racine de l'arbre
- 𝐻(x) = 1 + 𝐻(y) si y est le père de x
Attention : La convention utilisée ici est : Le niveau de la racine vaut 1 tandis que sa hauteur (ou sa profondeur) valent 0.
Pour l'instant nos arbres ne sont pas triés (il ne s'agit pas encore d'arbre binaire de recherche). Ainsi, pour savoir où se situe un noeud et en déduire sa hauteur (ou sa profondeur), il faut parcourir tout l'arbre à sa recherche. L'idée ici va être de descendre dans l'arbre, de manière récursive, en partant de la racine (hauteur 0, niveau 1). Pour chaque noeud rencontré, on va enregistrer dans un dictionnaire sa valeur et son niveau.
- S'approprier la méthode
hauteurNoeud(self, valeur). - Implémenter l'algorithme ci-dessous afin de compléter la méthode
_hauteursNoeuds(self, hauteurs, niv)qui permet, en parcourant l'arbre, de créer le dictionnaire {valeur du noeud : niveau du noeud} utilisé parhauteurNoeud(self, valeur). - Ajouter une méthode
niveauNoeud(self, valeur), utilisant la précédentehauteurNoeud(self, valeur)et qui retourne le niveau d'un noeud.
Pseudo code :
dicoN ← dictionnaire vide
a ← arbre binaire
h ← 0
FONCTION hauteursNoeuds(a, dicoN, h):
AJOUTER à dicoN, le couple (racine(a), h)
SI a A un sag :
dicoN ← hauteursNoeuds(sag(a), dicoN, h+1)
SI a A un sad :
dicoN ← hauteursNoeuds(sad(a), dicoN, h+1)
RETOURNER dicoNHauteur d'un arbre
Elle est définie par :
hauteur(self) qui retourne la hauteur de l'arbre.
Les arbres binaires de recherche (ABR)
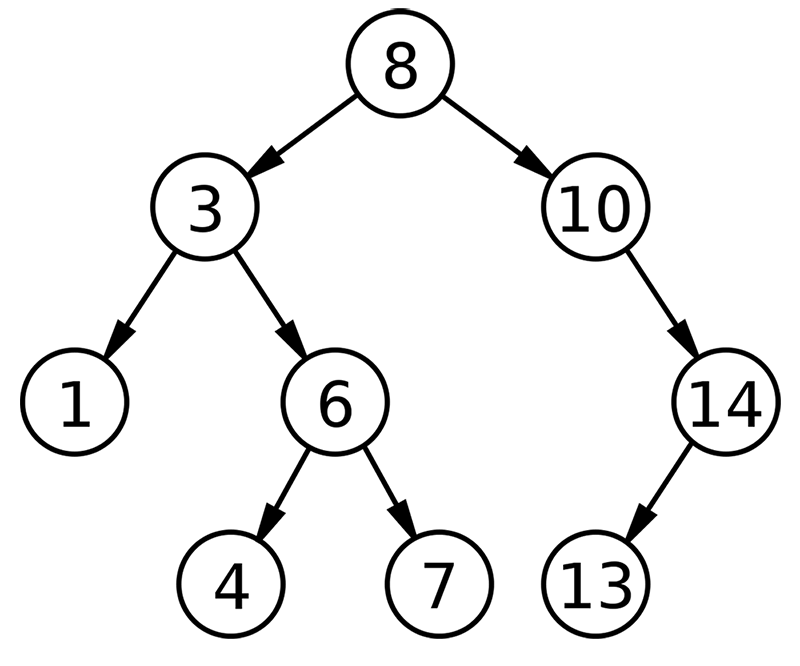
- Les valeurs du SAG doivent être inférieures à celle de la racine.
- Les valeurs du SAD doivent être supérieures à celle de la racine.
- À la main, à partir d'un arbre binaire de recherche vide, ajouter successivement les valeurs 23, 42, 15, 6, 18, 37, 53, 10, 26, 49 et 43.
- Combien de comparaisons effectuez-vous pour rechercher la valeur 6 dans cet arbre binaire de recherche ?
- Combien de comparaisons effectuez-vous pour rechercher la valeur 43 dans cet arbre binaire de recherche ?
Algorithmes sur les arbres binaires de recherche
Parcours des valeurs dans l'ordre croissant
Recherche d'une valeur
a ← arbre binaire de recherche
x ← valeur à rechercher
FONCTION rechercher(a, x) :
SI x = racine(a) ALORS
REPONDRE vrai
SINON SI x < racine(a) ALORS
SI a A un sag ALORS
recherche(sag(a), x)
SINON REPONDRE faux
SINON
SI a A un sad ALORS
recherche(sad(a), x)
SINON REPONDRE faux- Implémenter la méthode
rechercher(self, valeur). - Construire un arbre binaire de recherche avec au moins quatre entiers différents et tester votre implémentation.
Insertion d'une valeur
- Rechercher puis implémenter la méthode
ajouter(self, valeur)pour ajouter une valeur à un arbre binaire de recherche.# ajouter(arbre_binaire, valeur) → def ajouter(self, valeur): if valeur < self.racine(): if not self.sag(): self._gauche=Arbre(valeur) else: self.sag().ajouter(valeur) elif valeur > self.racine(): if not self.sad(): self._droit=Arbre(valeur) else: self.sad().ajouter(valeur) - Tester votre méthode sur l'arbre précédemment créé.
- Créer un nouveau fichier
tri.pydans le même dossier queTAD_Arbre.py. - Dans les premières lignes de ce fichier, importer le module
TAD_Arbre.py. - Puis écrire une fonction qui transforme une liste d'entier en un arbre binaire de recherche puis retourne la liste triée.
Recherche du minimum et du maximum
- Rechercher puis implémenter les méthodes
min(self)etmax(self)qui retournent respectivement la plus petite ou la plus grande valeur présente dans un ABR en exploitant ses propriétés pour être la plus efficace possible. - Tester vos méthodes sur l'arbre précédemment créé.
Aller plus loin !
Vérifier un ABR
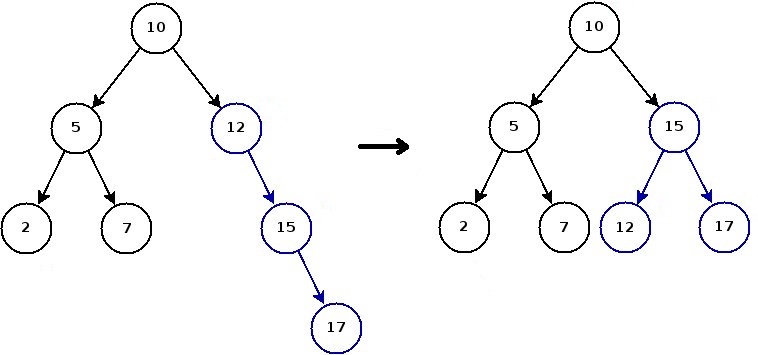
Suppression d'une valeur d'un ABR
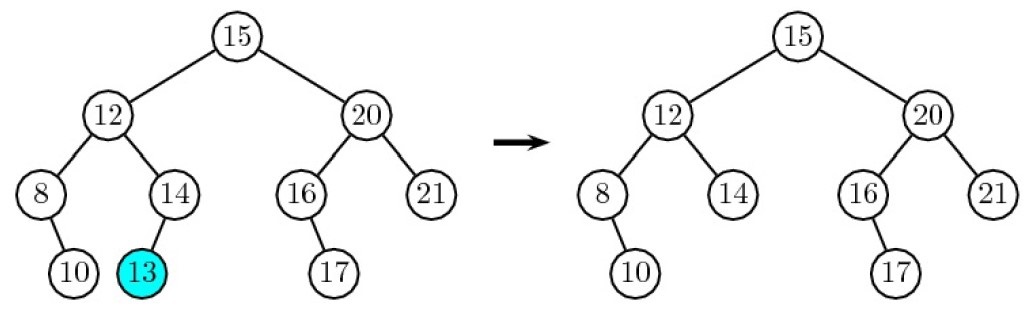
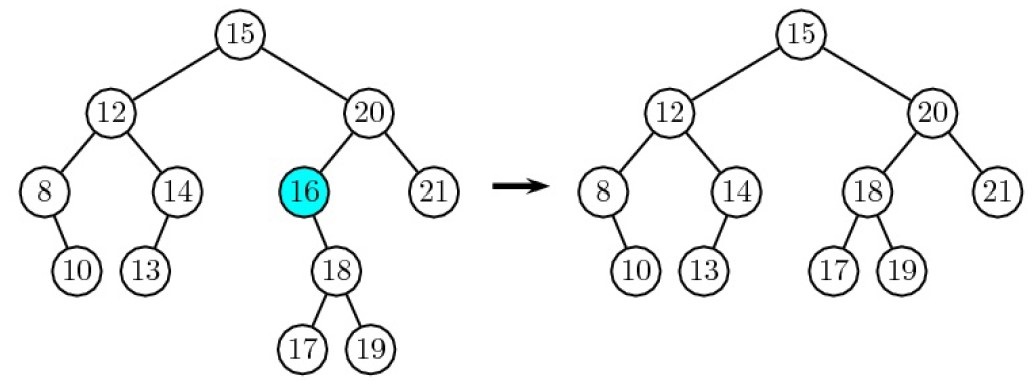
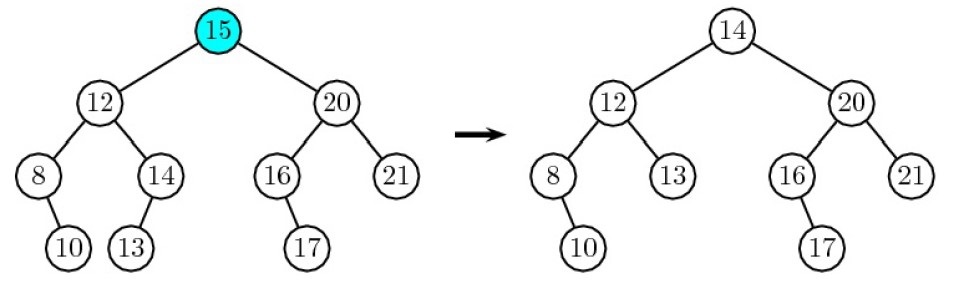
supprimer(self, x)- Rajouter un attribut
_parent__init__ - Modifier, lorsque c'est nécessaire, les méthodes écrites précédemment.
- Écrire une méthode
nombreFils(self, x) - Écrire les trois méthodes correspondant au troix cas expliqué précédement :
supprimeFeuille(self, x)supprimeUnFils(self,x)supprimeDeuxFils(self, x)
Équilibrer un ABR