1re NSI / Cours

1. Origine du binaire en informatique

Pour communiquer, deux êtres humains doivent parler la même langue. L'échange d'informations entre les composants d'un ordinateur repose sur le même principe.

Dans les années 40, lorsqu'il a fallu passer de l'idée abstraite de machine de Turing (modèle mathématique) à la réalisation concrète du premier ordinateur (machine physique), la question des composants matériels à choisir s'est posée (transistor, lampe, DEL, aimant, tube, bande, …). Pour ces composants, il est possible de réduire leur fonctionnement à 2 états exclusifs l'un de l'autre : état 0 et état 1.

le transistor est bloqué (état 0) ou passant (état 1),
la lampe est éteinte (état 0) ou allumée (état 1),
le ruban est trouée (état 0) ou non (état 1),
la bande magnétique présente un pôle Nord (état 0) ou Sud (état 1).

Le langage de base finalement choisie pour l'informatique, et encore utilisé aujourd'hui, est le binaire dont l'unité est le bit : binary digit (ou nombre binaire), pouvant prendre comme seules valeurs 0 ou 1.

Analogie : Notre langage humain occidental est lui basé sur 26 valeurs que sont les lettres de l'alphabet. En réalité plus, si l'on compte les accents, la ponctuation ...

Mémorisation 0x - Réussite 0/0/4

Démarrer

Combien d'état différents peuvent être définis avec un bits ?

2. Représentation binaire

Un ordinateur réalise des calculs, il faut donc être capable de convertir tous nos nombres habituels écrit en base décimale, sous forme de mots binaires composés uniquement d'une suite de 0 et de 1, c'est-à-dire écrits en base deux.

Pour nos nombres décimaux, le chiffre de poids le plus fort (ici la centaine) est placé à gauche :
Nombre décimal : 257₍₁₀₎ = (2 × 100) + (5 × 10) + (7 × 1) = (2 × 10²) + (5 × 10¹) + (7 × 10⁰)
Il en sera de même en binaire :
Nombre binaire : 1101₍₂₎ = (1 × 2³) + (1 × 2²) + (0 × 2¹) + (1 × 2⁰) = 2³ + 2² + 2⁰ = 8 + 4 + 1 = 13₍₁₀₎

Pour compter en binaire, il est alors important de connaître ses puissances de 2 par coeur :

2¹⁰	2⁹	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
1024	512	256	128	64	32	16	8	4	2	1

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0/10

Démarrer

Quel est la valeur décimale du nombre binaire 10₍₂₎ ?

À l'inverse, il faut être capable de trouver l'écriture binaire d'un nombre décimal :
Exemple :
26₍₁₀₎ = (1 × 2⁴) + 10
= (1 × 2⁴) + (1 × 2³) + 2 = (1 × 2⁴) + (1 × 2³) + (0 × 2²) + (1 × 2¹) + (0 × 2⁰)
= 11010₍₂₎

3. Méthode de conversion : décimal vers binaire

Méthode des divisions successives par deux :

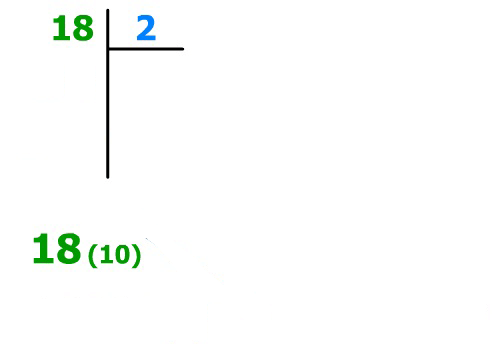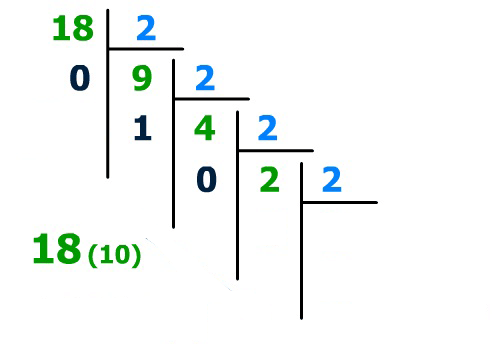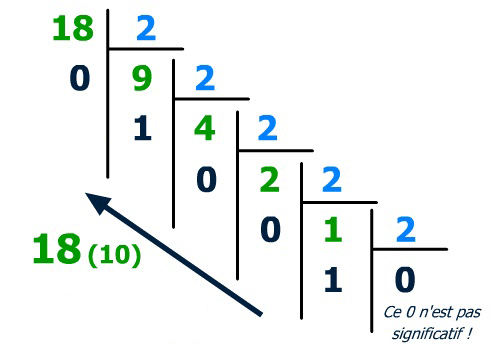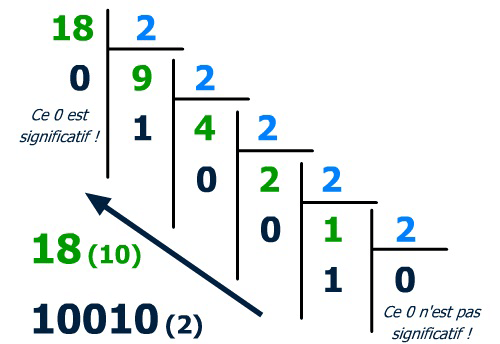
Réaliser des divisions successives sur le nombre décimal à convertir puis sur les quotients obtenus.
Dès que le quotient vaut 0, lire les restes obtenus de dernier au premier.

Méthode plus intuitive :

Écrire les puissances de 2 de droite à gauche jusqu'à atteindre la valeur du nombre décimal à convertir.
En commençant par la gauche, si la puissance de 2 est inférieure ou égale au nombre, inscrire 1 sous la puissance de 2 sinon 0 et calculer le reste.
Poursuivre ainsi en comparant les restes aux puissances de 2 jusqu'à atteindre 1=2⁰.

Mémorisation 0x - Réussite 0/0/9

Démarrer

Quel est la représentation binaire de la valeur décimale 255₍₁₀₎ ?

Donner votre réponse sur un minimum de bits et sans espace.

4. Représentation hexadécimale

L'hexadécimal est une représentation plus compacte des nombres. Elle n'est pas utilisée par les machines qui travaillent en binaire mais cette représentation a l'avantage d'être 4 fois plus courte à écrire, ce qui améliore sa lisibilité.

L'hexadécimal utilise 16 symboles : les dix chiffres (de 0 à 9) et les six premières lettres de l'alphabet en majuscule.

Base 10	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Base 16	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Base 2	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Conversion des entiers naturels de la représentation hexadécimale à la représentation décimale :
Exemple : A3₍₁₆₎ = 10 × 16¹ + 3 × 16⁰ = 10 × 16 + 3 × 1 = 160 + 3 = 163₍₁₀₎

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0/6

Démarrer

Quelle valeur décimale est représentée par A₍₁₆₎ ?

Pour convertir des entiers naturels de la représentation binaire à la représentation hexadécimale : Il suffit de regrouper les bits par quatre et de leur associer leur chiffre hexadécimal.
Exemple : 0110 1000 0010 1101₍₂₎ = 682D₍₁₆₎

Pour convertir de la base 10 vers la base 16, il sera souvent plus rapide de passer par la base 2 mais la méthode est similaire.

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0/6

Démarrer

Quelle est la représentation hexadécimale du nombre binaire 1010₍₂₎ ?

Compter en binaire c'est comme en décimal : dès que l'on a atteint le maximum (1 en binaire, 9 en décimal) sur un emplacement, il faut ajouter 1 sur l'emplacement à gauche et repartir de 0.

Décimal	0	1	2	3	4	5	6	7	8	9	10	...
Binaire	0	1	10	11	100	101	110	111	1000	1001	1010	...

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0

Démarrer

Compter en binaire jusqu'à 25.

11;12;13;14;15;16;17;18;19;20;21;22;23;24;25 1011;1100;1101;1110;1111;10000;10001;10010;10011;10100;10101;10110;10111;11000;11001

Passons aux additions :

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0

Démarrer

Poser puis réaliser l'addition décimale de « 23+14 » puis « 15+9 » comme appris en primaire.

Dans une addition avec des nombres binaires, il peut aussi y avoir des retenues, comme en décimal. En base 10, on ne peut pas dépasser le chiffre 9 et les retenues commencent donc à partir de 9. En base 2, on ne peut pas dépasser le chiffre 1 et les retenues commencent donc à partir du chiffre 1.

Exemple :

Mémorisation 0x - Réussite 0/0/7

Démarrer

Quel est le résultat binaire de l'addition : 1₍₂₎ + 1₍₂₎ ?

Remarque : La soustraction repose sur le même principe.

Mémorisation 0x - Réussite 0/0

Démarrer

Poser, comme en primaire, la soustraction décimale 453₍₁₀₎ - 99₍₁₀₎.

453₍₁₀₎ - 99₍₁₀₎ = 354₍₁₀₎

5. Codage des entiers relatifs (positifs et négatifs) : le binaire signé

Un ensemble de 8 bits forme un octet (appelé Byte en anglais à ne pas confondre avec un bit !).
1 octet = 8 bits

Code source (modification) : HTML MarkDown

Consulter le guide
sur Wikipédia.

Question

Écrire du HTML

Mémorisation 0x - Réussite 0/0

Démarrer

Sur un octet, il est possible de coder {rep1} valeurs différentes allant {rep2} (plus petite valeur) à {rep3} (plus grande valeur).

Pour coder les entiers négatifs, il faut coder le signe. Dans la représentation en binaire signé sur 8 bits, le bit de poids le plus fort sert à coder le signe. 1 codant pour un entier négatif et 0 pour un entier positif.

Exemple : Pour une représentation binaire signé sur 1 octet : −4₍₁₀₎ = 1000 0100_(2𝑠)

Mémorisation 0x - Réussite 0/0/16

Démarrer

Quelle est la représentation en binaire signé sur 8 bits de la valeur décimale 1₍₁₀₎ ?

6. Codage des entiers relatifs : le complément à 2

Pour conserver la propriété d'addition sur les entiers relatifs en binaire, une autre méthode de représentation existe : le complément à 2.
Pour obtenir le complément à 2 d'un nombre :

s'il est positif, on prend sa représentation en binaire simple,
s'il est négatif, on prend son complément à 1 (en inversant tous les bits : 1 devient 0 et 0 devient 1) et on additionne 1. (Cela revient à inverser que les bits de gauche à droite jusqu'au dernier 1 rencontré que l'on n'inverse pas.)

Le bits de poids le plus fort donne l'information du signe comme en binaire signé : 1 pour – et 0 pour +.

Exemple :
4₍₁₀₎ = 0000 0100₍₂₎ = 0000 0100_(c2) et -4₍₁₀₎ = 1111 1100_(c2)
11₍₁₀₎ = 0000 1011₍₂₎ = 0000 1011_(c2) et -11₍₁₀₎ = 1111 0101_(c2)

Mémorisation 0x - Réussite 0/0

Démarrer

Quel est l'avantage du complément à deux sur le binaire signé pour coder les entiers relatifs ?

C'est plus rapide à coder.

C'est plus simple à coder.

Il permet de garder la propriété d'addition des nombres en binaire.

Cocher la bonne réponse.

→ Voir la vidéo : Twos complement: Negative numbers in binary de Ben Eater

7. Codage des réels : virgule fixe

7.1. Principe

Tous les réels ne vont pas pouvoir être codés. La puissance des ordinateurs étant limitée, il ne va pas être possible d'écrire les réels possédant un nombre infini de chiffre après la virgule, tel que π. Leur représentation sera toujours une approximation.
Pour convertir la partie fractionnaire d'un nombre, en binaire, il faut utiliser les puissances de 2 négatives.

$2^{- 1}$	$2^{- 2}$	$2^{- 3}$	$2^{- 4}$	$2^{- 5}$	$2^{- 6}$	$2^{- 7}$	$2^{- 8}$
0,5	0,25	0,125	0,0625	0,03125	0,015625	0,0078125	0,00390625

Cette méthode de codage à virgule fixe reprend le principe du binaire signé :

le premier bit code le signe (1 pour – et 0 pour +)
une partie des bits suivants codent pour la partie entière (pondération des puissances positives de 2)
et les autres pour la partie fractionnaire (pondération des puissances négatives de 2).

Pour un codage sur 1 octet (8 bits) : 1 bit de signe / 3 bits de partie entière / 4 bits de partie fractionnaire
Pour un codage sur 2 octets (16 bits) : 1 bit de signe / 7 bits de partie entière / 8 bits de partie fractionnaire

Exemple :
Pour un codage sur 16 bits à virgule fixe : +10, 25₍₁₀₎ = 0000 1010, 0100 0000_(2fix)
Pour la partie entière : 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰ = 8 + 2 = 10
Pour la partie fractionnaire : 0 × 2⁻¹ + 1 × 2⁻² = 0 × 0,5 + 1 × 0,25 = 0,25

1 min Mémorisation 0x - Réussite 0/0/8

Démarrer

Quelle est la représentation en binaire signé à virgule fixe sur 8 bits, de la valeur décimale 0,5 ?

7.2. Méthode de conversion de la partie fractionnaire : de décimal vers binaire

Pour convertir un nombre fractionnaire en binaire, il faut réaliser des multiplications successives par deux, des parties fractionnaires, en gardant la partie entière des résultats. Dans la plupart des cas, la méthode entraîne une boucle : le résultat sera une suite se répétant à l'infini. Ainsi, la représentation sur un nombre fini de bits introduit obligatoirement une approximation.

Exemple :

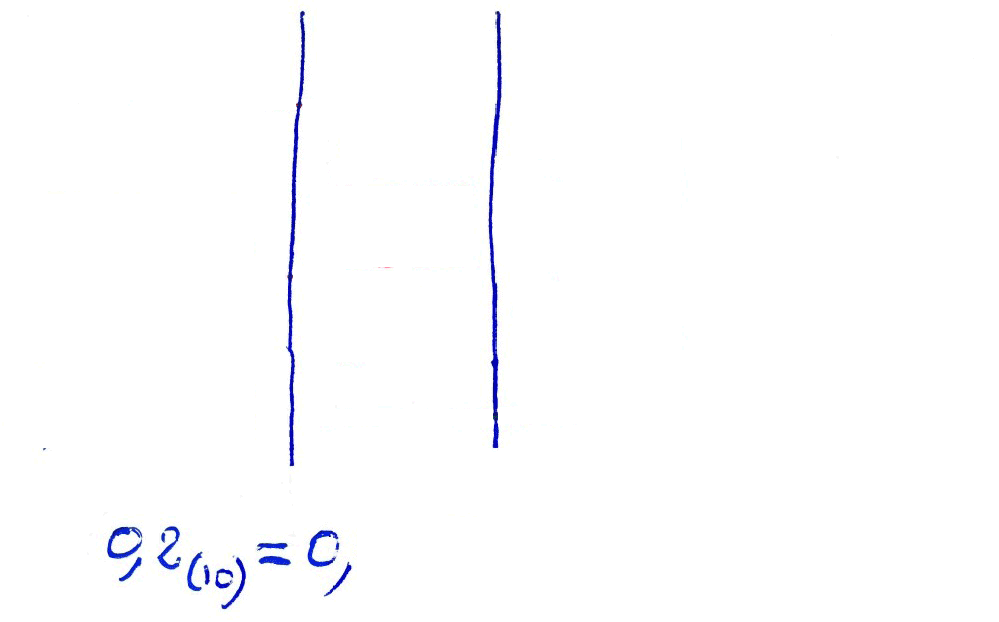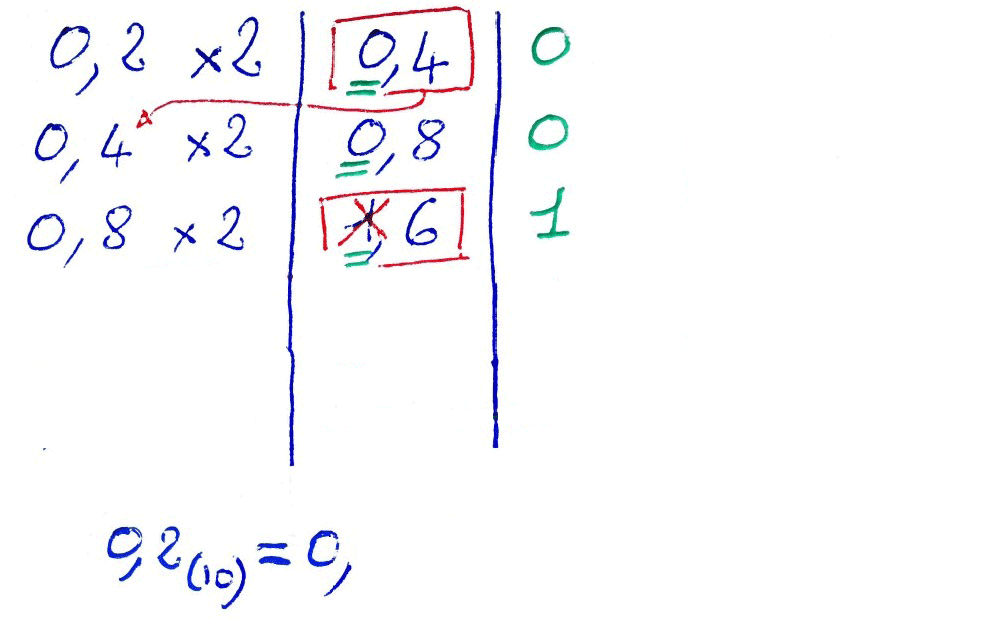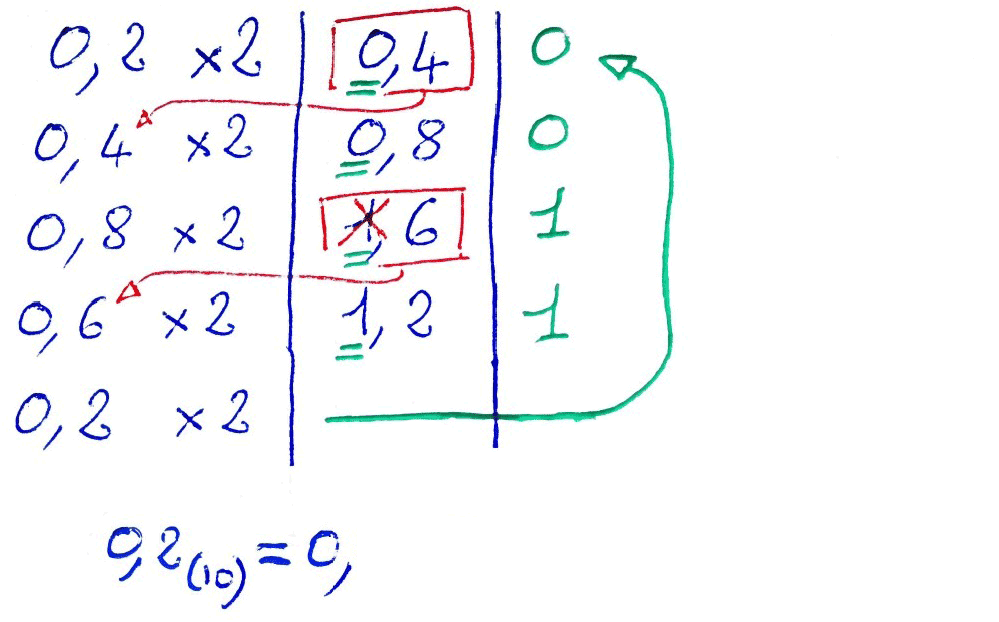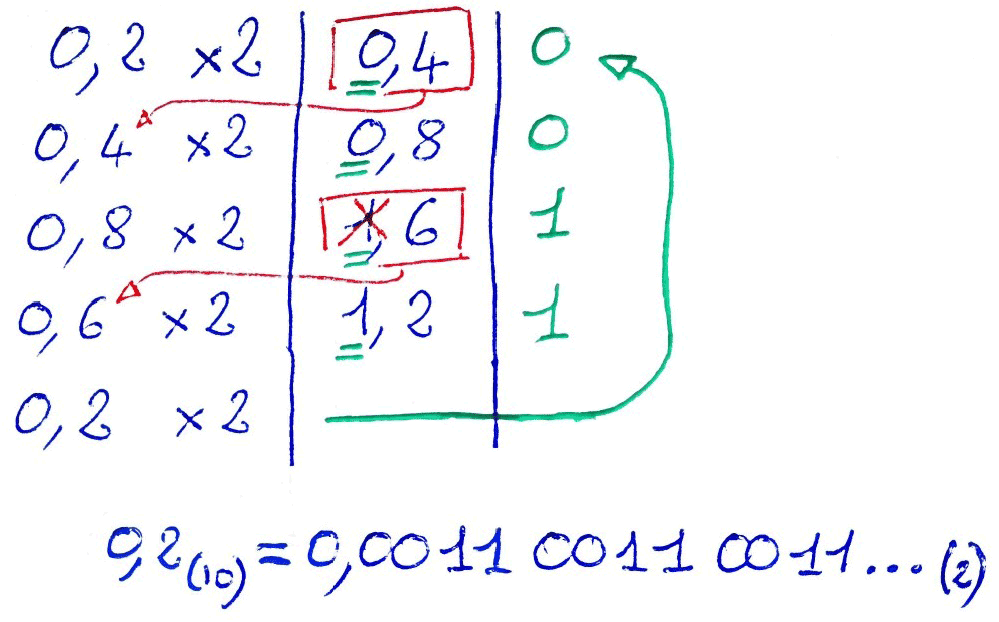
Méthode de conversion de la partie fractionnaire
(Image cliquable)

Le résultat s'écrit en binaire :
0,2₍₁₀₎ = 0,0011 0011 0011 0011 0011...₍₂₎

en binaire à virgule fixe sur 16 bits :
0,2₍₁₀₎ = 0000 0000, 0011 0011_(2fix)

Mémorisation 0x - Réussite 0/0/14

Démarrer

Donner la représentation en binaire signé à virgule fixe sur 8 bits de la valeur décimale 0,6₍₁₀₎ ?

En programmation, il sera dangereux de vérifier l'égalité de deux nombres à virgule.
Rappelez-vous que certaines valeurs ne sont pas représentables parfaitement en binaire. De la même façon que

\frac{1}{3}

n'est pas représentable en décimal car cela nécessiterait d'écrire

0, 333 ...

suivi d'une infinité de

3

ce qui est impossible, certains nombres ne sont pas représentables parfaitement en binaire et seront donc représentés de manière approchée.

8. Codage des réels : virgule flottante

La technique de représentation des nombres à virgule fixe est simple mais l'ensemble des valeurs représentables est très limité du fait des bits souvent perdus à gauche ou à droite. Une autre technique est celle des nombres à virgule flottante.

Pour représenter un nombre binaire à virgule flottante, il faut d'abord l'exprimer en notation scientifique binaire sous la forme : $mantisse \times 2^{exposant}$ . La mantisse est obligatoirement supérieure à 1.
Sur 8 bits, la représentation binaire à virgule flottante se compose de : 1 bit pour le signe / 3 bits pour l'exposant / 4 bits pour la partie fractionnaire de la mantisse

Exemple : 2,625₍₁₀₎ = 10,101₍₂₎ = 1,0101₍₂₎ × 2¹ = 0100, 0101_(2flo)

Le 1 de la partie entière de la mantisse est systématique, il est donc inutile de le coder.
L'exposant peut être négatif donc pour permettre de coder autant d'exposants positifs que négatifs sur seulement 3 bits (soit 8 valeurs possibles), la norme IEEE-754 impose d'ajouter 3 à l'exposant.
Dans notre cas, l'exposant est 1₍₁₀₎ donc 1 + 3 = 4₍₁₀₎ = 100₍₂₎.

Mémorisation 0x - Réussite 0/0

Démarrer

Dans la représentation binaire à virgule flottante sur 8 bits,

la partie fractionnaire n'est pas codée, car elle vaut toujours 1.

la partie entière n'est pas codée, car elle vaut toujours 1.

il faut soustraire 3 à la valeur qu'il faut coder pour l'exposant.

il faut ajouter 3 à la valeur qu'il faut coder pour l'exposant.

la partie fractionnaire n'est pas codée, car elle vaut toujours 0.

la partie entière n'est pas codée, car elle vaut toujours 0.

Cocher la ou toutes les bonnes réponses.

La norme IEEE-754 est réellement définie sur 32 ou 64 bits, ce qui permet d'écrire de très grands nombres.

→ Pour aller plus loin, voir la vidéo : Decimal to IEEE 754 Floating Point Representation de Abishalini Sivaraman

9. Codage des caractères

Dans un second temps, les informaticiens ont commencé à vouloir coder non seulement les nombres mais aussi l'ensemble des caractères. Une première table de correspondance associant à chaque caractère (a, b, !, espace, virgule, …) un mot binaire de 7 bits, a été établie. Cette table a été définie en 1960 et est encore utilisée aujourd'hui. C'est la table ASCII :

Caractère ASCII (Langage humain)	Code ASCII décimal	Mot binaire de 7 bits (Langage machine)
a	97	110 0001
?	63	011 1111

→ Voir la table complète sur Wikipédia.

Afin de pouvoir coder les caractères européens (accent, cédille, …), une autre norme a été définit en 1986. Elle s'appelle ISO-8859-1 ou Latin-1. Chaque caractère est alors codé sur 8 bits.

Ces systèmes de codage ont encore évolué afin d'inclure de plus en plus de caractère. La norme Unicode (ou UTF-8) vise à coder tous les caractères du globe et pour cela, elle est capable d'adapter le nombre de bits nécessaire à l'alphabet de 1 à 4 octets.

Exemple : Voici quatre exemples de codage en UTF-8 de caractère :

A est codé par 0100 0001₍₂₎ = 41₍₁₆₎
Ω est codé par 1100 1110 1010 1001₍₂₎ = CE A9₍₁₆₎
∞ est codé par 1110 0010 1000 1000 1001 1110₍₂₎ = E2 88 9E₍₁₆₎
𐎄 est codé par 1111 0000 1001 0000 1000 1110 1000 0100₍₂₎ = F0 90 8E 84₍₁₆₎

Format de fichier texte

Créer un fichier texte .txt (clic droit / nouveau / document texte) et y écrire la lettre «a». Enregistrer-le (enregistrer sous / format ANSI/ASCII) et déterminer sa taille c'est-à-dire le nombre de bits ou d'octets nécessaires pour le coder (clic-doit / propriétés). Comment justifier son poids ?
Le fichier texte contenant une lettre fait 1 octet ce qui correspond bien à son codage UTF-8 sur 8 bits.
Prévoir la taille d'un fichier texte contenant la phrase « Salut tout le monde ! ». Vérifier votre hypothèse.
Ce fichier devrait faire 21 octets car il comporte 21 caractères.
Enregistrer cette fois un fichier contenant la même phrase mais LibreOffice (en .odt) ou OnlyOffice (en .docx). Que constate-t-on ?
Le même fichier est bien plus lourd car il contient des informations sur la mise en forme utilisée.
Essayer d'ouvrir le fichier .txt avec LibreOffice. Inversement essayer d'ouvrir le fichier .docx ou .odt avec le bloc-note. Que constate-t-on ?
Word ou LibreOffice sont capable de lire un fichier .txt mais le traitement de texte de base n'est pas capable de lire un fichier .docx ou .odt.

Mémorisation 0x - Réussite 0/0

Démarrer

Combien de caractère peut contenir la table ASCII originelle utilisant 7 bits ?

→ Voir le site : Convertisseur de code Unicode