1re NSI / Cours

Algorithme

Que veut dire « Savoir programmer » ?

L'informatique a pour objectif de faire réaliser par une machine des tâches répétitives de façon automatique. Face à cela, plusieurs questions se posent et notamment celle de la communication avec l'ordinateur. Rappelons en effet que l'ordinateur ne manipule que des 0 et des 1 (le binaire est le langage avec le plus bas niveau d'abstraction) tandis que l'être humain peut exprimer ses idées à l'aider de phrases complexes (plus haut niveau d'abstraction).

Exemple de programmation :

Langage humain (plus haut niveau d'abstraction) :
Demander l'âge et répondre "Vous êtes mineur." lorsqu'il est inférieur à 18 et "Vous êtes majeur." sinon.
Traduire en pseudo-code :
Dans un premier temps, il faut traduire cette tâche en une suite d'instructions simples et sans ambigüités (on parle d'instructions élémentaires et univoques). La façon de résoudre cette tâche est alors un algorithme. Il peut exister plusieurs algorithmes plus ou moins performants permettant de résoudre une même tâche.
```
# Pseudo-langage (haut niveau d'abstraction)
Demander un entier et l'affecter à age
si age est inférieur à 18 alors
 répondre "Vous êtes mineur."
sinon
 répondre "Vous êtes majeur."
```
Implémenter (traduire dans un langage choisi) :
Un algorithme écrit en pseudo-langage, est encore très éloignés du langage machine. Il est nécessaire de le traduire dans un langage commun, avec une syntaxe : c'est le langage de programmation. Ces langages sont nombreux et variés (Python, C, C++, Pascal, Java, PHP, Kotlin, …) et se prêtent plus ou moins bien à la tâche.
```
# Python (assez haut niveau d'abstraction) :
age = input("Quel est votre âge ?")
if int(age) < 18:
 print("Vous êtes mineur.")
else:
 print("Vous êtes majeur.")
```
```
// Javascript (assez haut niveau d'abstraction) :
var age = prompt("Quel est votre âge ?");
if (age < 18) {
 alert("Vous êtes mineur.");
} else {
 alert("Vous êtes majeur.");
}
```
Interpréter/Compiler/Assembler (traduire en langage machine) :
Pour que l'algorithme soit exécuté par le processeur, il doit être traduit en langage machine : le binaire. Il s'agit du langage de plus bas niveau d'abstraction.
Certains langages sont dit interprétés (comme python). Dans ce cas, un interpréteur traduit ligne par ligne le code python en langage machine. Sans l'interpréteur installé sur le poste, ce type de langage n'est pas exécutable directement.
D'autres sont dit compilés (comme C). Un compilateur crée un exécutable (langage assembleur) qui n'a plus besoin d'un autre logiciel pour être exécuté. Une dernière étape, appelée l'assemblage, permet de traduire le langage assembleur en langage machine.
```
#Langage machine (binaire) (plus bas niveau d'abstraction) :
001010001010001000011101110010100010100110101011
100110010010100101010010010101001111011010101101
000101010100101001001010010101110110100101001010
010111101101010111010101001010111111111111110001
```

Plus on se rapproche du langage machine, plus on descend dans les niveaux d'abstraction.
Plus un langage est compréhensible par un humain, plus son niveau d'abstraction est élevé.

Finalement, apprendre à programmer c'est savoir :

Formuler une tâche sous la forme d'un algorithme.
Implémenter un algorithme dans un langage de programmation.

Complexité d'un algorithme

La rapidité d'un ordinateur dans l'exécution d'un algorithme dépend de la fréquence de calcul de son processeur, mais aussi de la complexité de l'algorithme utilisé.

La complexité (temporelle) d'un algorithme est le nombre d'opérations élémentaires (affectations, comparaisons, opérations arithmétiques) effectuées.
Ce nombre s'exprime en fonction de la taille 𝑛 des données à traiter et permet d'estimer le coût en calcul d'un algorithme.

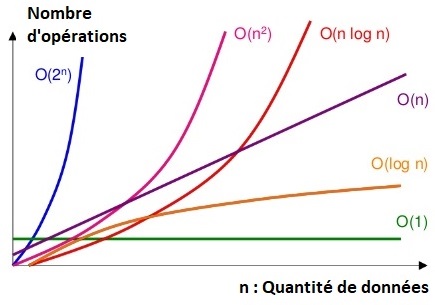
Cette fonction est notée sous la forme 𝑂(𝑛) « grand 𝑂 de 𝑛 » et indique en quelque sorte « l'ordre de grandeur » de la complexité de l'algorithme.

Déterminer la complexité d'un algorithme permet de le comparer aux autres afin de déterminer lequel est le plus performant.

La recherche de l'algorithme ayant la plus faible complexité, pour résoudre un problème donné, fait partie du travail régulier de l'informaticien. Il est aidé pour cela par les mathématiciens.

Un algorithme de complexité linéaire 𝑂(𝑛) nécessite un nombre d'opérations proportionnel à la quantité de données (taille du problème) : 𝑛.
Un algorithme de complexité quadratique 𝑂(𝑛²) nécessite un nombre d'opérations proportionnel au carré de la quantité de données : 𝑛².
Vous rencontrerez également des complexités constantes 𝑂(1), linéarithmiques 𝑂(𝑛log(𝑛)) ou exponentielles 𝑂(2^𝑛).

Un algorithme de complexité linéaire est plus performant qu'un algorithme de complexité quadratique.

Retrouver les différents types de complexité sur : Analyse de la complexité des algorithmes (Wikipédia)

Classer les algorithmes du plus lent au plus rapide pour résoudre un grand problème de taille n selon leur complexité : : 𝑂(log(𝑛)), 𝑂(𝑛²), 𝑂(𝑛), 𝑂(1) et 𝑂(𝑛log(𝑛)).

Évaluer rapidement la complexité de ces algorithmes :

```
print("Hello world!")
```
La complexité est constante 𝑂(1) .
```
for element in liste : # liste contient n éléments
 ...
```
On parcours une fois tous les éléments de la liste : la complexité est linéaire 𝑂(𝑛) .
```
for element in liste : # liste contient n éléments
 for element in liste :
 ...
```
Pour chaque élément de la liste, on parcours de nouveau tous les éléments de la liste : la complexité est quadratique 𝑂(𝑛²) .
```
for i in range(len(liste)) : # liste contient n éléments
 for element in liste[i+1:] :
 ...
```
Pour chaque élément de la liste, on parcours tous les éléments qui le suivent dans la liste. Ainsi plus on avance dans la première boucle, plus la deuxième boucle est courte ; malgré ceci, la complexité est quadratique 𝑂(𝑛²) : exemple sur 5 instructions au début :
```
.....
 ....
 ...
 ..
 .
```
(demi carré)

def fibo(n) :
 """ Calcul du n-ième terme de la suite de fibonaci par une méthode récursive"
 if n <= 1: # Cas triviaux (multiple)
 return n
 else: # Cas récursif double
 return fibo(n-2) + fibo(n-1)

Preuve d'un algorithme

Pour tester si vos programmes fonctionnent, vous le testez avec quelques exemples. Or, vous savez que mathématiquement et d'un point de vue logique, un exemple ne suffit souvent pas à constituer une preuve générale. Le nombre de tests à réaliser pour prouver un programme devrait être infini. Ce qui est dans la pratique impossible.

Pourquoi s'assurer de la preuve du bon fonctionnement d'un algorithme ? Il existe malheureusement des exemples où une erreur informatique a pu coûter cher, en matériel (explosion de Ariane 5 en 1996) et parfois en vies humaines (crash du Boeing 737 Max en 2018). On peut aussi comprendre que le logiciel impliqué dans la sécurité d'une centrale nucléaire doit être sans faille.

La preuve d'un algorithme est constituée de deux éléments à valider séparément :

La preuve de terminaison : Un programme doit avoir une fin : toutes les conditions d'arrêt doivent pouvoir être remplies au cours de l'exécution. Un programme n'est jamais infini : même en cas d'exécution en continu, il doit exister un bouton d'arrêt (condition de terminaison).
La preuve de correction : En supposant qu'il termine, le programme doit bien réaliser ce pour quoi il a été écrit.

Faillir à une seule de ces deux conditions remet en question la validité de l'algorithme.

Exemple simple : Calcul de la longueur du segment [AB] dans le plan

Algorithme :

xA, yA, xB, yB sont des nombres
longueurAB = sqrt ((xB – xA)**2 + (yB – yA)**2)

Preuve de terminaison : Il y a un nombre fini d'opérations, sans boucle ni tests, le programme terminera.
Preuve de correction : Une propriété mathématique démontrée assure la correction de la formule utilisée.

Exemple avec une boucle : Calcul de la somme des éléments d'une liste numérique

Algorithme :

liste ← une liste numérique
somme ← 0
pour i allant de 0 à longueur de liste - 1
	somme ← somme + liste[ i ]
afficher somme

Preuve de terminaison : La boucle POUR est exécutée autant de fois qu'il y a de valeurs dans liste. On peut utiliser ici ce qu'on appelle un variant de boucle. C'est une variable dont la valeur change, toujours dans le même sens (augmente ou diminue) à chaque itération de la boucle et qui en atteignant une valeur finale, assure la terminaison. Dans le cas d'une boucle pour, le variant de boucle est facile à trouver car le nombre d'étapes est connu à l'avance. Cela est en général moins évident dans le cas d'une boucle while.
Preuve de correction : Dans le cas d'une boucle, on utilise la méthode de l'invariant de boucle. C'est une propriété qui est vraie avant et après chaque répétition (précondition de boucle, conservation pour chaque itération de la boucle et postcondition de boucle). Ici l'invariant pourrait être : somme est bien la somme des éléments parcourus jusqu'à présent.
- Précondition de boucle : somme vaut 0 pour aucun élément parcouru. C'est vrai pour i = 0 (en maths, on parle d'initialisation).
- Conservation : Si on considère un i tel que somme est bien la somme des éléments jusqu'à i. En passant à i+1, on ajoute à somme l'élément i + 1, somme représente donc bien la somme des i + 1 premiers éléments de liste. En mathématiques on dit que la propriété est héréditaire.
- Postcondition de boucle : Le raisonnement précédent est un raisonnement par récurrence, il assure que le résultat est vrai pour tous les éléments de liste. Ceci assure la preuve de correction de cet algorithme.

Traduire l'algorithme de calcul de la somme des éléments d'une liste en python.

def somme(liste):
    som = 0
    for val in liste:
        som += val
    return som

Insérer des assertions dans votre code, pour vérifier l'invariant de boucle.

def somme(liste):
    """Calcule la somme des valeurs de la liste"""
    som = 0

    # Précondition sur l'invariant de boucle
    i = 0
    assert som == 0, "Erreur sur la précondition de l'invariant de boucle"

    for val in liste:
        som += val

        # Conservation de l'invariant
        assert som == sum(liste[0:i + 1]), "Non-conservation de l'invariant de boucle"
        i += 1

    # Postcondition sur l'invariant de boucle
    assert som == sum(liste), "Erreur sur la postcondition de l'invariant de boucle"

    return som

Algorithmes de recherche

Algorithme de recherche séquentielle

Prenons 7 cartes portant un numéro différent compris entre 1 et 10 (Jeu de 54 cartes). Les cartes sont désordonnées et retournées face cachée. L'objectif est de retrouver la carte portant le numéro 4.

Proposer un algorithme pour retrouver la carte.
Les unes après les autres on retourne les cartes et on compare leur valeur à la valeur recherchée jusqu'à ce qu'elle soit trouvée.

Implémenter (traduire) votre algorithme de recherche en python.

def recherche_sequentielle(liste, element):
 for i, val in enumerate(liste):
 if val == element: return i
 return False

Combien d'opérations sont nécessaires dans le meilleur et dans le pire des cas ?
Dans le meilleur des cas (la valeur recherchée est la première carte), il faut 1 lecture et 1 comparaison soit 2 opérations.
Dans le pire des cas (la valeur recherchée est sur la dernière carte), il faut 7 lectures et 7 comparaisons soit 14 opérations.
Quelle est la complexité de cet algorithme appelé algorithme de recherche séquentielle ?
Le nombre d'opération à effectuer est au pire proportionnel au nombre de carte.
La complexité de l'algorithme de recherche séquentielle est linéaire. Cela signifie que le nombre d'opérations à effectuer (ou le temps d'exécution) est proportionnel à la taille des données.

Algorithme de recherche dichotomique

Considérons désormais 7 cartes triées par ordre croissant.

Proposer un meilleur algorithme que le précédent pour trouver la carte numéro 4 dans ce jeu trié.
- Quand le liste est triée, commencer par lire la carte du milieu et comparer sa valeur à la valeur recherchée.
- Si la valeur lue est plus grande, éliminer toute la deuxième moitié du paquet
- sinon éliminer toute la première moitié du paquet et recommencer avec la moitié restante.
Combien d'opérations sont nécessaires dans le meilleur et dans le pire des cas ?
- Dans le meilleur des cas (la valeur recherchée est la première carte retournée), il faut 1 lecture et 1 comparaison soit 2 opérations.
- Dans le pire des cas (la valeur recherchée est sur la dernière carte retournée), il faut 3 lectures et 3 comparaisons soit 6 opérations
Comparer les performances de l'algorithme de recherche dichotomique avec celles de l'algorithme de recherche séquentielle.
L'algorithme de recherche dichotomique a une complexité logarithmique en 𝑂(log(𝑛)). Il est plus performant que l'algorithme de recherche séquentielle mais nécessite que le tableau soit trié.

L'idée de l'algorithme de recherche dichotomique date de l'antiquité (-220) dans la ville mésopotamienne : Babylone. Il applique le principe du diviser pour régner (divide and conquer) qui permet généralement d'obtenir de meilleurs algorithmes.
La méthode "diviser pour régner" se déroule en 3 étapes :

Diviser : Découper le problème initial en sous-problème.
Régner : Résoudre les sous-problèmes.
Combiner : Calculer la solution du problème initial à partir des solutions des sous-problèmes.

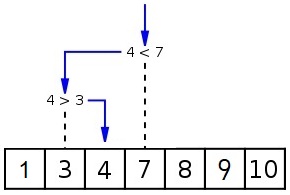
Illustration de la recherche par dichotomie

Algorithme de recherche dichotomique :

liste ← liste de valeurs triée
valeur ← la valeur à chercher
a ← 0 (indice du 1re élément de la liste)
b ← longueur de liste – 1 (indice du dernier élément de la liste)
m ← (a+b)//2 (indice de l'élément au milieu de la liste)
tant que a < b
 si liste[m] est égal à valeur
 répondre m
 si liste[m] > valeur
 b ← m-1
 sinon
 a ← m+1
 m ← (a+b)//2
fin tant que
répondre a

Preuve de terminaison :
Les variables a et b sont deux entiers naturels, par conséquent l'écart b - a est aussi un entier naturel et celui-ci décroit à chaque itération car soit b diminue, soit a augmente. Ainsi, il existe une itération pour laquelle b - a sera négatif et la boucle TANT QUE s'arrêtera. L'écart b - a est le variant de boucle.

L'algorithme présenté ci-dessus assure-t-il que la valeur recherchée est dans la liste ?
Non, cet algorithme ne vérifie pas que le dernier élément de la liste correspond bien à la valeur recherchée. Cet algorithme est bon quand on est sûr que la valeur recherchée est dans la liste car elle permet de gagner deux opérations.

Implémenter l'algorithme de recherche dichotomique en python.

def recherche_dichotomique(liste_triee, valeur):
 a = 0
 b = len(liste_triee) - 1
 m = (a + b) // 2
 while a < b:
 if liste_triee[m] == valeur:
 return m
 elif liste_triee[m] > valeur:
 b = m - 1
 else:
 a = m + 1
 m = (a + b) // 2
 if liste_triee[m] == valeur:
 return m
 else:
 return -1 # absent de la liste

Insérer des assertions dans votre code pour vérifier le variant de boucle.

def recherche_dichotomique2(liste_triee, valeur):
 """Renvoie l'indice de la valeur recherchée dans la liste triée."""
 a = 0
 b = len(liste_triee) - 1
 m = (a + b) // 2

 # Variant de boucle
 d0 = b - a

 while a < b:
 if liste_triee[m] == valeur:
 return m
 elif liste_triee[m] > valeur:
 b = m - 1
 else:
 a = m + 1
 m = (a + b) // 2

 # Vérification du variant de boucle
 d1 = b - a
 assert d1 < d0, "La variant n'évolue pas !"
 d0 = d1

 if liste_triee[m] == valeur:
 return m
 else:
 return -1 # absent de la liste

Autres algorithmes de recherche

On peut aussi imaginer des algorithmes de recherche qui nécessitent un traitement des données.

Proposer un algorithme de recherche d'un extremum (maximum ou minimum) puis l'implémenter en python.

def recherche_min(liste):
 if len(liste) == 0:
 return None
 rep = float("+inf")
 for val in liste:
 if val < rep:
 rep = val
 return rep

def recherche_max(liste):
 if len(liste) == 0:
 return None
 rep = float("-inf")
 for val in liste:
 if val > rep:
 rep = val
 return rep

Proposer un algorithme de calcul d'une moyenne puis l'implémenter en python.
Parcourir la liste de valeur en les additionnant. À la fin, diviser le résultat de la somme par le nombre de valeurs sommées.
```
def moyenne(liste):
 if len(liste) == 0:
 return None
 som = 0
 for val in liste:
 som += val
 return som/len(liste)
```
Évaluer la complexité de ces deux algorithmes.
Ces deux algorithmes parcourent une seule fois la liste. Le nombre d'opération est proportionnel au nombre d'élément dans la liste donc la complexité est linéaire 𝑂(𝑛) .

Algorithmes de tri

Reprenons 5 cartes portant chacune un numéro différent compris entre 1 et 10 (Jeu de 54 cartes). Les cartes sont désordonnées et retournées face cachée. L'objectif est de les trier.

Proposer un algorithme permettant de les trier.

Il existe un grand nombre d'algorithme de tri que vous pouvez découvrir en allant sur le site interstices.

Tri par sélection

Cet algorithme de tri est le plus naturel. Son principe consiste à rechercher la plus petite valeur (ou la plus grande) de la liste et à la placer en premier (ou en dernier), et ainsi de suite …

Voir le tri par sélection interprété par des danseurs folkloriques Gypsy : Youtube

Il existe deux variantes pour ce tri :

« sur place » où la liste est modifiée en échangeant ses valeurs de place dans la même liste,
« par copie » où une nouvelle liste est créée pour y ranger les valeurs au fur et à mesure.

Laquelle des variantes est la plus performante ?

Pseudo-code de l'algorithme de tri par sélection :

L ← liste de nombres
pour i allant de 0 à longueur(L) - 2
 indiceMin ← i
 pour j allant de i + 1 à longueur(L) - 1
 si L[ j ] < L[indiceMin] alors indiceMin ← j
 fin pour
 échanger L[i] et L[indiceMin]
fin pour

Implémenter l'algorithme de tri par sélection en python.

def tri_selection(liste):
 for i in range(len(liste)-1):
 imin = i
 for j in range(i+1, len(liste)):
 if liste[j] < liste[imin]:
 imin = j
 liste[i], liste[imin] = liste[imin], liste[i]
 return liste

Évaluer la complexité de cet algorithme.
Pour chaque élément de la liste, il faut parcourir presque tous les autres éléments pour les comparer entre eux soit environ n x n opérations. Ainsi la complexité de l'algorithme de tri par sélection est quadratique 𝑂(𝑛²) .
Justifier la terminaison du tri par sélection à l'aide d'un variant de boucle.
La preuve de terminaison est qu'ici la valeur 10×𝑖 + 𝑗 augmente à chaque itération pour atteindre une valeur finale. 10×𝑖 + 𝑗 est notre variant de boucle qui assure la terminaison de l'algorithme.
Décrire un invariant de boucle qui prouve la correction de l'algorithme de tri par sélection.
À chaque itération la liste liste[0:i] est triée.

Tri par insertion

Cet algorithme de tri est relativement naturel. Son principe est le suivant : Pour chaque élément de la liste, on le compare à tous ceux qui le précèdent jusqu'à déterminer sa bonne position (entre un plus petit et un plus grand que lui) et l'y insérer.

Décrire l'algorithme du tri par insertion en pseudo-langage.

L ← une liste de nombres
pour i allant du deuxième terme à la fin de la liste
 v ← L[i]
 j ← i-1
 tant que j est positif et que v < L[i]
 décaler le terme d'indice j en j+1
 décrémenter j
 fin tant que
 place v en position d'indice j+1 dans la liste
fin pour

Implémenter (traduire) l'algorithme de tri par insertion en python.

def tri_insertion(liste):
 for i in range(1, len(tab)):
 k = tab[i]
 j = i-1
 while j >= 0 and k < tab[j] :
 tab[j + 1] = tab[j]
 j -= 1
 tab[j + 1] = k

Évaluer la complexité de cet algorithme.
Pour chaque élément de la liste, il faut parcourir presque tous les autres éléments pour les comparer entre eux soit environ 𝑛×𝑛 opérations. Ainsi la complexité de l'algorithme de tri par insertion est quadratique 𝑂(𝑛²) . Il existe un cas où elle est linéaire 𝑂((𝑛)) , c'est lorsque la liste est presque déjà ordonnée.
Justifier la terminaison du tri par insertion à l'aide d'un variant de boucle. Réponse La preuve de terminaison est qu'ici la valeur 10×𝑖 + 𝑥 augmente à chaque itération pour atteindre une valeur finale. 10×𝑖 + 𝑥 est notre variant de boucle qui assure la terminaison de l'algorithme.
Décrire un invariant de boucle qui prouve la correction de l'algorithme de tri par insertion
À chaque itération la liste liste[0:i] est triée.

la complexité des algorithmes de tri par sélection et par insertion est quadratique : 𝑂(𝑛²).
Ils sont tous deux peu efficaces lorsque le nombre de données devient important.

Remarque :

Le principe « diviser pour régner » peut être appliqué dans le domaine des tris notamment avec le tri fusion de complexité linéarithmique 𝑂(𝑛log(𝑛)) et qui sera étudié en terminale.

Visualiser différents tris sur www.toptal.com.

Algorithmes gloutons

Les algorithmes gloutons répondent à des problèmes d'optimisation. L'idée est qu'à chaque étape de l'algorithme, celui-ci fasse le choix qui lui semble le plus optimal, sans réfléchir à la suite, en espérant que la solution finale au problème soit elle-même la plus optimale. Attention cela n'est pas forcément toujours le cas et dépend du problème à traiter.
L'exemple classique d'application d'un algorithme glouton est le problème du rendu de monnaie. L'objectif est, à partir d'un système de monnaie, de trouver comment rendre une somme de façon optimale, c'est-à-dire avec le moins de pièces et de billets possible.

Résoudre le problème de rendu de monnaie avec un algorithme glouton en pseudo-langage.

POUR chaque type de monnaie présent dans la caisse, de la plus grande à la plus petite :
 TANT QUE la valeur à rendre est supérieur à la valeur de la monnaie :
 Compter le nombre de cette monnaie à rendre
 Soustraire la valeur de la monnaie à la somme à rendre

Implémenter l'algorithme glouton du rendu de monnaie en python.

def rendre_monnaie(caisse, x):
 """Calcul d'un rendu de monnaie en fonction des valeurs de monnaie disponible
 dans la liste caisse et de la valeur à rendre x."""
 n = len(caisse)
 choix = [0] * n # Pour stocker le nombre de chaque type de monnaie à rendre
 ###################
 # A VOUS DE JOUER #
 ###################

 return choix

# Batterie de tests
caisse = [500, 200, 100, 50, 20, 10, 5, 2, 1]
assert rendre_monnaie(caisse, 800) == [1, 1, 1, 0, 0, 0, 0, 0, 0]
assert rendre_monnaie(caisse, 6) == [0, 0, 0, 0, 0, 0, 1, 0, 1]
assert rendre_monnaie(caisse, 49) == [0, 0, 0, 0, 2, 0, 1, 2, 0]

def rendre_monnaie(caisse, x):
 """Calcul d'un rendu de monnaie en fonction des valeurs de monnaie disponible
 dans la liste caisse et de la valeur à rendre x."""
 n = len(caisse)
 choix = [0] * n
 for i in range(n):
 while x >= caisse[i]:
 x -= caisse[i]
 choix[i] += 1
 return choix

def traduire_rendu(caisse, choix):
 """Traduit le choix de rendu en français."""
 for i in range(len(choix)):
 if choix[i] != 0:
 print("Rendre",choix[i],'de',caisse[i],"euros.")

# Batterie de tests
caisse = [500, 200, 100, 50, 20, 10, 5, 2, 1]
assert rendre_monnaie(caisse, 800) == [1, 1, 1, 0, 0, 0, 0, 0, 0]
assert rendre_monnaie(caisse, 6) == [0, 0, 0, 0, 0, 0, 1, 0, 1]
assert rendre_monnaie(caisse, 49) == [0, 0, 0, 0, 2, 0, 1, 2, 0]

Bon à savoir : Le système de monnaie a été choisi pour qu'un algorithme glouton soit optimal.

Un exemple pour comprendre :
Comment payer 9€ avec un système de pièces ou de billets de 1€, 2€, 5€ et 10€ ?
Le choix optimal (moins de pièces et de billet) s'obtient en appliquant l'algorithme glouton (choisir toujours la plus grande des valeurs pour compléter) : soit 5€ + 2€ + 2€ (3 pièces).

Imaginons qu'il existe un billet de 7€. L'algorithme glouton n'est plus optimal. En effet si l'on souhaite payer 14€, il donnerait : 10€ + 2€ + 2€ alors que le meilleur choix serait 7€ + 7€.

Un autre problème où l'on peut appliquer un algorithme glouton est le problème du sac à dos. Vous disposez d'un ensemble d'objets unique définit par une masse et une valeur pécuniaire et d'un sac à dos ne pouvant transporter qu'une certaine masse. L'objectif est de définir quels objets mettre dans le sac en maximisant la valeur de l'ensemble.

Résoudre le problème du sac à dos avec un algorithme glouton en pseudo-langage.

Implémenter l'algorithme glouton pour le problème du sac à dos en python.

def remplir_sac(objets, m):
    """Donne le meilleur choix des objets à prendre dans la sac
       pour maximiser la valeur transportée."""
    choix = [0] * len(objets)
    ###################
    # A VOUS DE JOUER #
    ###################

    return choix

# Batterie de tests

objets = [[5, 0.5], [3, 4], [2, 1], [1, 0.2]]     # [[valeur, masse], ...]
assert remplir_sac(objets, 5.0) == [1, 1, 0, 1]

objets = [[6, 5.0], [5, 5.0], [4.5, 2.0], [4, 2.0], [3, 8.0], [1, 2.0], [0.5, 3.0]]
assert remplir_sac(objets, 5.0) == [1, 1, 1, 1, 1, 0, 0]

Algorithmes des k plus proches voisins

Abrégé en KNN (K-nearest neighbors), cet algorithme cherche à prédire la classe (ou propriété) d'un élément en fonction de la classe majoritaire de ses k plus proches voisins.
Par exemple, imaginons qu'un pixel soit manquant dans une image. L'algorithme va prédire la couleur de ce pixel en fonction de la couleur des pixels voisins.
L'algorithme KNN est un algorithme d'apprentissage (Machine Learning) supervisé. C'est-à-dire qu'à partir d'un ensemble des données étiquetées, il va pouvoir prédire l'étiquette d'une donnée inconnue.
Par exemple, à partir d'un ensemble d'images de chiens et de chats, ce type d'algorithme permet de déterminer si une photo inconnue est celle d'un chien ou d'un chat.
Un autre exemple sont les systèmes de recommandation. Un site marchand peut chercher vos k plus proches voisins en termes d'âge, de lieu, etc., pour vous proposer des articles susceptibles de vous plaire.

point ← point de référence
k ← nombre de voisins souhaité
liste ← liste des points donnés
liste_points_distances ← liste vide
POUR tous les points dans la liste :
 d ← distance entre le point de la liste et le point de référence
 ajouter le point de la liste et sa distance au point de référence dans liste_points_distance
FIN POUR
trier liste_indices_distances selon leur distance au point de référence
renvoyer les k premiers points de liste_points_distance

Récupérer et s'approprier les fichiers : 04_algorithme_KNN.py et liste_10pts.csv.

Implémenter (traduire) l'algorithme KNN en python en complétant la fonction


recherche_KNN(point, liste, k)

.

def recherche_KNN(point, liste, k):
 """Renvoie la liste des k plus proches voisins du point : [x, y],
 dans la liste de point donnee :
 [[nom1, x1, y1, couleur1], [nom2, x2, y2, couleur2], ...]."""
 liste_points_distances = []
 for p in liste:
 coord = (p[1], p[2])
 d = calculer_distance(point, coord)
 liste_points_distances.append((p, d))
 voisins = sorted(liste_points_distances, key=lambda x: x[1])[:k] # Trie les éléments de voisins selon d croissant
 return voisins

Compléter les fonctions calculer_distance(p1, p2) et completer_KNN(liste, k) pour obtenir une image complète.

def calculer_distance(p1, p2):
 """Calcule la distance entre les points p1 et p2 : [x, y]."""
 distance = ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5
 return distance


def completer_KNN(liste, k):
 """Colore tous les points manquants de l'image."""
 liste_complete = []
 i = 0
 x_max = max(liste, key=lambda x: x[1])[1]+1
 y_max = max(liste, key=lambda y: y[2])[2]+1
 for x in range(x_max):
 print(str(x*100//x_max)+"%") # Affichage de la progression du calcul
 for y in range(y_max):
 voisins = recherche_KNN([x, y], liste, k)
 if x == 9 and y == 19:
 b=3
 couleur_retenue = predire_couleur(voisins)
 liste_complete.append(["P"+str(i), x, y, couleur_retenue])
 return liste_complete