Chapitre 8 : Algorithmique
Remarque : Survoler les termes soulignés pour en obtenir plus d'informations.
Nous allons voir dans ce cours des techniques d'optimisation. Optimiser une solution, c'est la rendre plus rapide car plus efficace. Elle vise à utiliser des raccourcis ou à éviter des opérations inutiles ou redondantes. Dans le cas de la récursivité, elle permet de simplifier le code et d'éviter certains bugs (effets de bords). Optimiser conduit ainsi souvent à améliorer la complexité d'un algorithme et donc sa rapidité d'exécution. En première, vous avez vu le cas de l'algorithme de recherche séquentielle de complexité linéaire `O(n)` et celui de la recherche dichotomique de complexité logarithmique `O(log(n))` qui était plus efficace.
Voir l'article sur l'Analyse de la complexité algorithmique (Wikipédia)
Récursivité
Un algorithme (ou fonction) récursif est un algorithme (ou fonction) qui fait appel à lui-même.
Nous allons voir qu'il existe différents types de récursivité : simple, double/multiple, imbriquée et mutuelle/croisée.
Récursivité simple
Exemple avec la fonction factorielle
En mathématique, la factorielle est définie par : `n! =
1xx2xx3xx...xxn` avec `n in NN`. Pour programmer récursivement, il faut être capable de découper le problème en sous-problèmes plus simples. À partir de là, il faut distinguer deux cas :
Dans l'exemple de la fonction factorielle : |
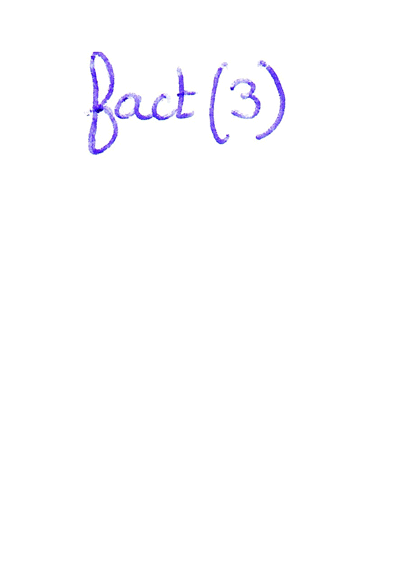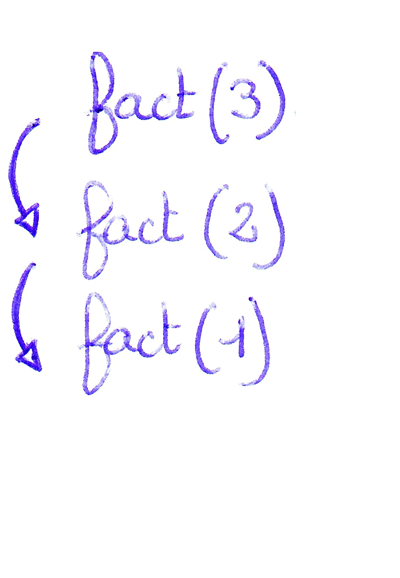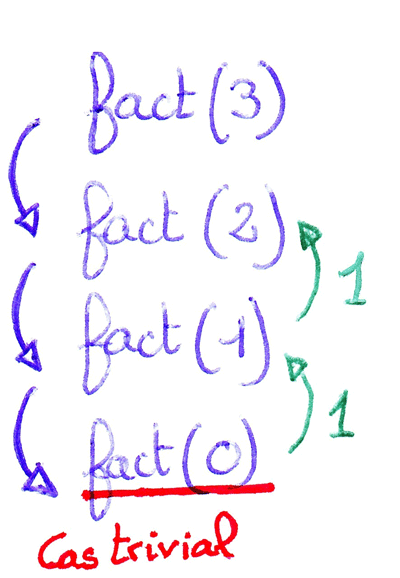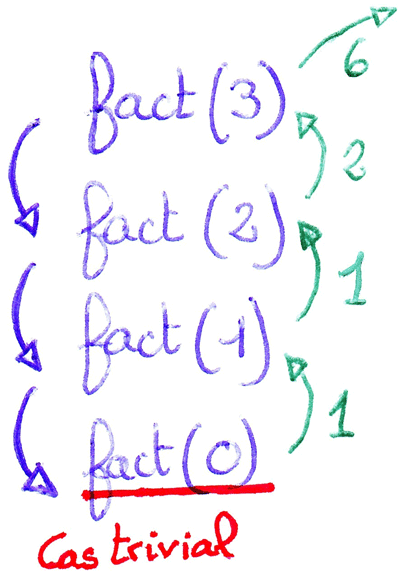
fact(3)Cliquer pour stopper l'animation. |
Cas de base/cas trivial multiples - Exemple avec la fonction factorielle
Pour la fonction factorielle, il est possible de définir un deuxième cas
de base : celui ou `n = 1` :
`fact(n) = {(1,si, n in [0, 1]),(nxxfact(n-1),si,n > 0):}`
cela permet d'optimiser l'algorithme en évitant un appel récursif.
Cas récursifs/cas non-trivial mutiples - Exemple avec la suite de syracuse
Remarque : Ici, il n'y a toujours qu'un seul appel récursif à la fois mais qui dépend du contexte. Cela diffère de la récursion multiple que nous allons voir par la suite.
La suite de Syracuse d'un nombre entier `N>0` est définie par récurrence
de la manière suivante :
`u_0 = N`
`u_(n+1) = {(u_n/2,si, u_n, est, pair),(3xxu_n+1,si,
u_n, est, impair):}`
Quel que soit la valeur de départ `N`, la suite
finie toujours par atteindre `1`. Le nombre d'étape pour atteindre la
valeur `1` est appelée le temps de vol. La plus grande valeur de la suite
obtenue est appelée l'altitude maximale.
1 - Implémenter en python la fonction `syracuse(n)` qui renvoie la liste des valeurs de la suite de syracuse allant de `n` à `1` en utilisant une boucle `text(while)`.
def syracuse(n):
tab = [n]
while n!=1:
if n%2 == 0:
n = n//2
else:
n = 3*n + 1
tab.append(n)
return tab2 - Implémenter la version récursive : `text(syra_recursif)(n)`.
def syra_recursif(n, tab=[]):
tab.append(n)
if n == 1: # Cas trivial
return tab
elif n%2 == 0: # Cas récursif 1 (multiple)
return syra_recursif(n//2)
else: # Cas récursif 2
return syra_recursif(n*3+1)3 - Améliorer la fonction pour qu'elle donne également le temps de vol et l'altitude maximale.
Récursion double - Exemple de la suite de Fibonacci
On parle de récursion double quand le cas récursif fait deux fois
appel à la fonction. L'exemple le plus connu est la suite de
Fibonacci. Sa définition récursive est :
|

fibo(5)Cliquer pour stopper l'animation. |
Récursion mutuelle (ou croisée)
Il s'agit de deux fonctions qui s'appellent mutuellement, c'est-à-dire que la première appelle la deuxième et la deuxième, la première.
Écrire les fonctions
pair et
impair mutuellement récursives, sans utiliser le modulo
% ni le not, telles que, étant donné un entier
n ≥ 0 : •
pair(n) retourne True si n est
pair et False sinon. •
impair(n) retourne True si n est impair et
False sinon.
def pair(n):
if n == 0:
return True
return impair(n-1)
def impair(n):
if n == 0:
return False
return pair(n-1)
Récursion imbriquée - Exemple avec la fonction d'AckermannUn appel récursif est dit imbriqué quand il apparaît en tant qu'argument d'un appel récursif.
La fonction d'Ackermann est définie mathématiquement par :
La seule opération effectuée lors du déroulement de la fonction d'Ackermann est l'ajout de 1 (lorsque m est nul). Malgré cela, cette fonction croît extrêmement rapidement : `acker(4,2)` a déjà 19729 chiffres ce qui représente bien plus que le nombre d'atomes estimé dans l'univers. 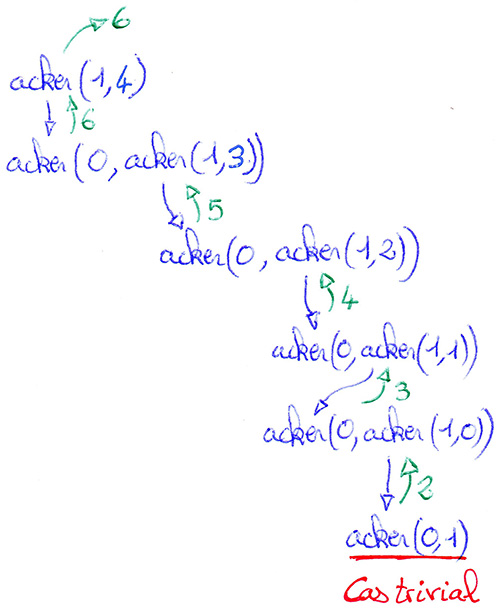 - quand `m = 0` - quand `m > 0 text( et ) n = 0` - quand `m > 0 text( et ) n > 0` |
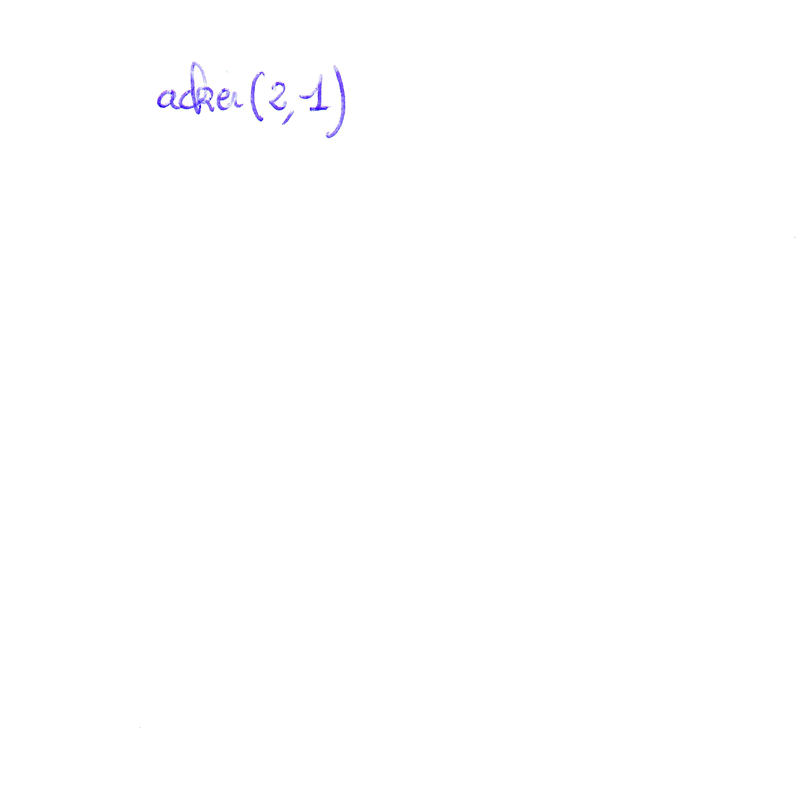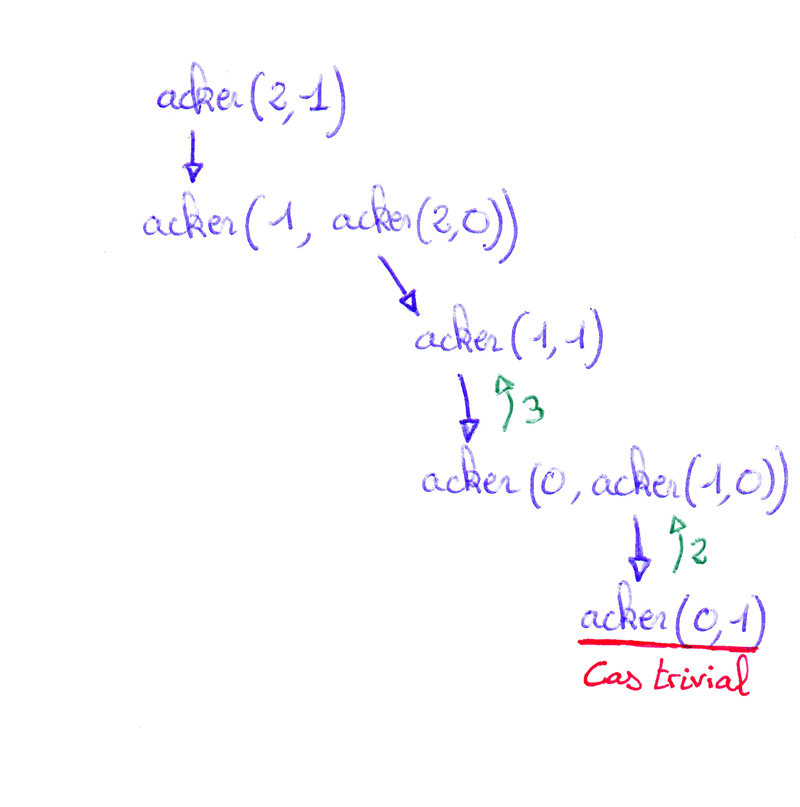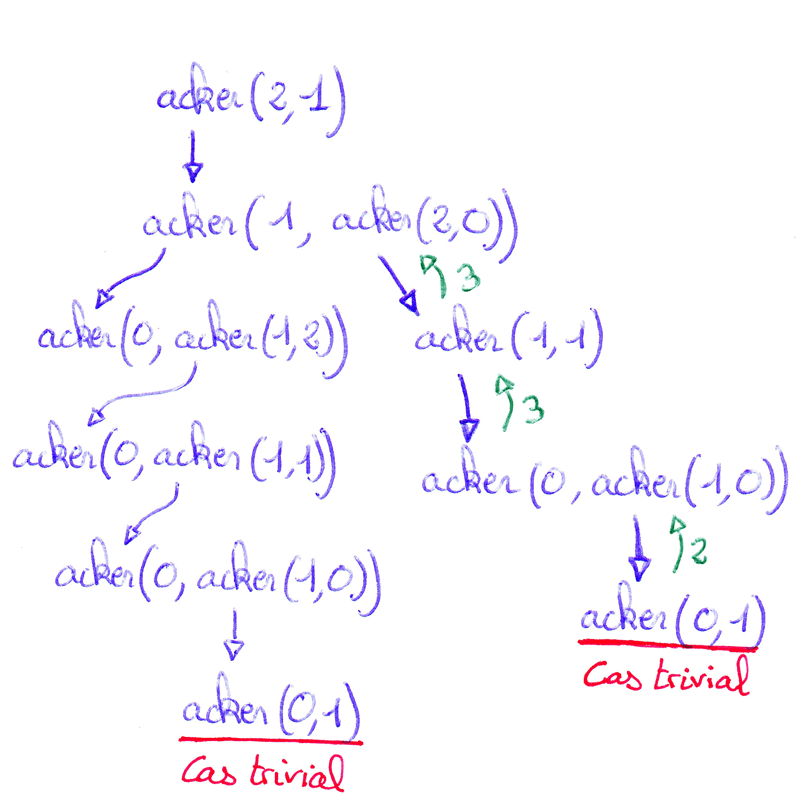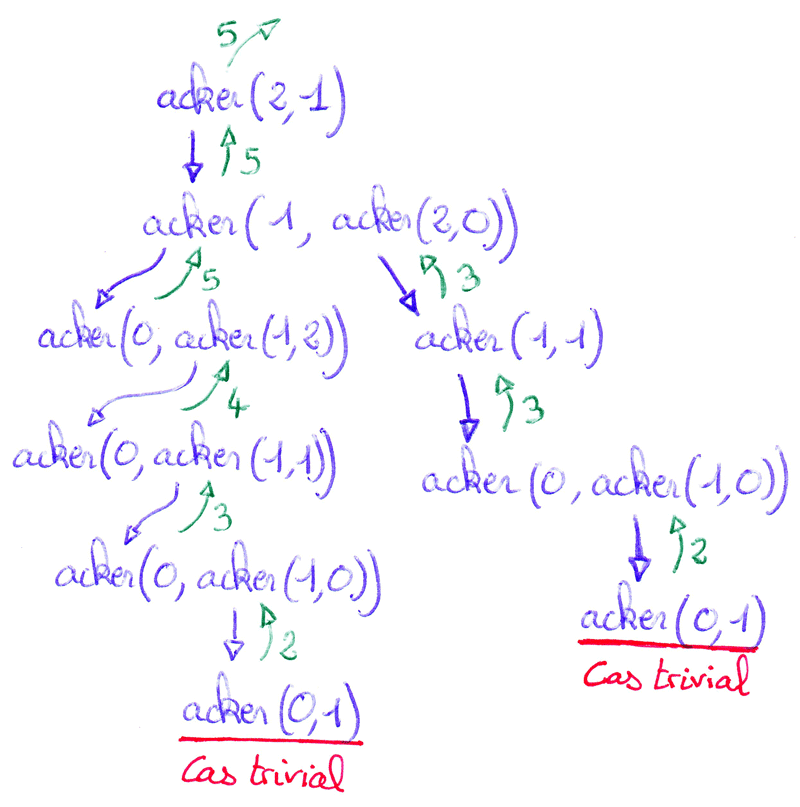
Cliquer pour stopper l'animation. |
Complexité d'un algorithme récursif
Un programme récursif a une complexité linéaire `O(n)` dans le cas ou sa
pile d'exécution est linéaire. C'est le cas de la fonction factorielle où
le nombre d'appels récursifs est proportionnel à la taille du problème
qui est ici le nombre dont on veut calculer la factorielle.
Dans le cas de la suite de Fibonacci, la pile d'exécution n'est pas
linéaire car on a affaire à une récursion double. Chaque appel entraine un
double appel récursif ce qui conduit rapidement à une explosion des appels
de la fonction. La complexité est alors exponentielle `O(2^n)`. Ici la
taille du problème de rang `n` correspond au rang de la suite que l'on
souhaite atteindre. Nous verrons par la suite que la
programmation dynamique permet d'optimiser l'algorithme
pour le rendre plus efficace.
La récursivité ne permet pas toujours d'apporter une meilleure réponse au problème. Dans le cas de la suite de Fibonacci, il est possible d'obtenir une complexité en `O(n)` par simple itération (avec une boucle `text(while)`).
Pour comparer deux algorithmes, une bonne méthode est de les soumettre à un même problème (même taille) et de chronométrer leur temps de réponse. Ce temps de calcul est proportionnel au nombre d'opérations effectuées ce qui est une bonne représentation de la complexité relative d'algorithmes.
def fibo_it(n):
tab = [1, 1]
while len(tab )< n:
tab.append(tab[-2]+tab[-1])
return tab[-1]
import time
def fibo_it(n):
tab = [1, 1]
while len(tab )< n:
tab.append(tab[-2]+tab[-1])
return tab[-1]
def fibo(n) :
if n <= 1: # Cas triviaux (multiple)
return n
else: # Cas récursif double
return fibo(n-2) + fibo(n-1)
for fct in [fibo_it, fibo]:
n = 30
start = time.time()
fct(n)
end = time.time()
print("Temps d'exécution de "+fct.__name__+"("+str(n)+") : "+str(end-start)+" s")
Correction d'un algorithme récursif
Deux propriétés doivent être vérifiées pour s'assurer qu'un algorithme récursif fonctionne correctement :
- sa terminaison : est-ce qu'il se termine ?
- sa correction partielle : fait-il ce qu'il est censé faire ? Dans le cadre d'un algorithme récursif, si les appels récursifs font ce que l'on attend d'eux, alors l'algorithme tout entier fera ce qu'il est censé faire. Cela ressemble au raisonnement par récurrence vu en mathématiques.
Exemple : Dans le cas de la fonction factorielle, sa
terminaison est assurée car la fonction prend en argument un entier
positif, l'appel récursif prend en argument l'entier décrémenté de 1 et le
cas d'arrêt est défini quand l'argument devient nul.
Sa correction
partielle consiste à s'assurer qu'un appel récursif renvoie bien :
`nxxfact(n-1)`
Limitation de l'interpréteur python
Par défaut, python limite le nombre d'appels récursifs d'une fonction à
1000. Au-delà, l'interpréteur python lève l'exception
RecursionError et affiche le message :
Recursion Error: maximum recursion depth exceeded.
Pour augmenter cette limite, il faut utiliser la fonction
setrecursionlimit(5000) du module sys. Cette
solution sera de courte durée face à la limite de puissance du processeur
et au temps d'exécution, en particulier avec des algorithmes de complexité
exponentielle.
import sys
sys.setrecursionlimit(5000)
Des langages utilisant le paradigme fonctionnel sont plus adaptés à
l'utilisation de la récursivité. En effet, pour certains cas, ils sont
capables d'éviter de multiplier les environnements d'appels dans la pile
des appels récursifs.
Exemple :
Langage OCaml
Méthode "Diviser pour régner"
La méthode "Diviser pour régner" est composées de trois phases :
- la division : le problème initial est divisé en sous-problèmes de tailles inférieures
- le règne : chaque sous-problème est résolu soit récursivement, soit directement s'il sont élémentaires
- la combinaison : les solutions des sous-problèmes sont combinées pour obtenir la solution du problème initial
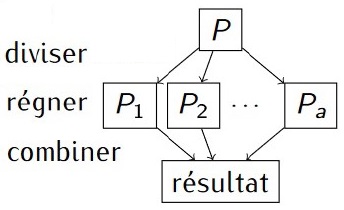
|
`P` est un problème de taille n |
La récursivité est tout à fait adaptée à la méthode "Diviser pour Régner" du fait quelle divise un problème initial en sous-problèmes.
Application avec le tri fusion
Pour trier un paquet de copie par ordre alphabétique, une idée assez
naturelle est de scinder le paquet en deux sous-paquets de même
taille, puis de trier chaque sous-paquets avant de les fusionner
pour obtenir un paquet trié. L'algorithme récursif est assez naturel :
Pseudo code : L'algorithme du tri fusion.
FONCTION tri_fusion(liste):
liste est la liste à trier
N ← longueur de la liste
Si N est nul ou vaut 1 alors retourner la liste telle quelle.
Sinon :
M ← Entier(N/2)
liste1 ← liste des M premiers éléments de liste
liste2 ← les éléments restant de la liste
Renvoyer la fusion de tri_fusion(liste1) et tri_fusion(liste2)
|
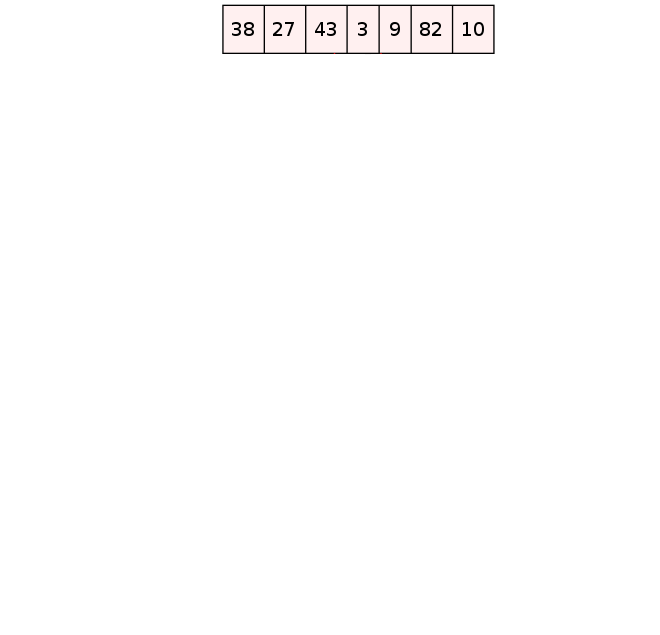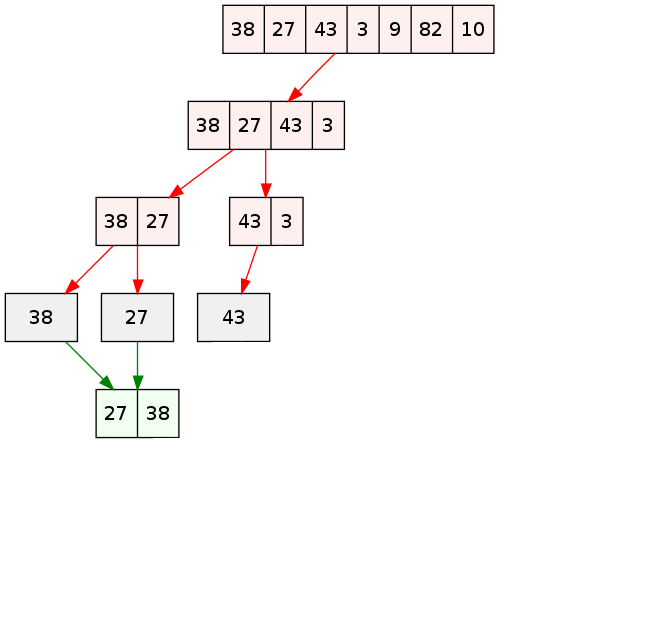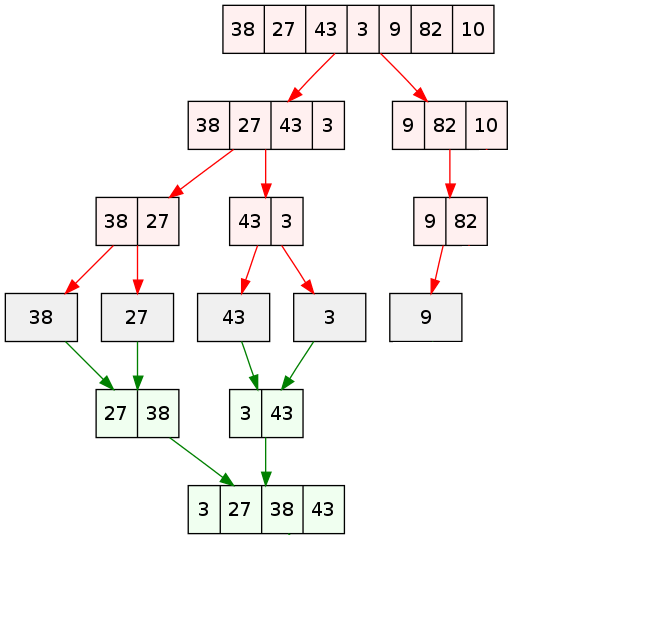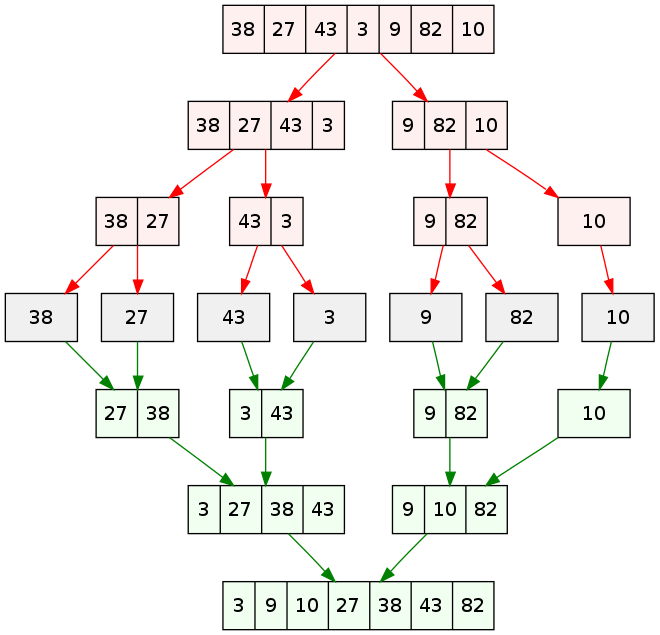
Cliquer pour stopper l'animation. |
fusionqui à partir de deux listes
triées, les fusionne pour obtenir une seule liste triée.
def fusion(l1, l2):
i1, i2, n1, n2 = 0, 0, len(l1), len(l2)
liste = []
while i1 < n1 and i2 < n2: # Jusqu'à épuisement d'une des liste
if l1[i1] < l2[i2]:
liste.append(l1[i1])
i1+=1
else:
liste.append(l2[i2])
i2+=1
if i1 == n1: # Puis on ajoute le reste
liste.extend(l2[i2:])
else:
liste.extend(l1[i1:])
return liste2 - Écrire la fonction
tri_fusionqui implémente le
pseudo-code présenté ci-dessus.
def tri_fusion(li):
n = len(li)
if n < 2:
return li
else:
m = n // 2
return fusion(tri_fusion(li[:m]), tri_fusion(li[m:]))Rappel de 1re : Les algorithmes de tri simple tels que le tri à bulle (par propagation), tri par insertion et tri par sélection nécessitent de parcourir tout ou partie de la liste pour chaque élement de la liste. Cela qui conduit à une complexité quadratique `O(n^2)`. Le tri fusion est plus efficace. Sa complexité est linéarithmique `O(n*log(n))`.
Application avac la rotation de 90° d'une image bitmapImage bitmapLes images bitmap (aussi appelées images raster) sont des images consituées de pixels, c'est-à-dire d'un ensemble de points structurés dans un tableau. Chacun de ces points possède une ou plusieurs valeurs décrivant sa couleur. Les images vectorielles sont constituées d'entités géométriques telles qu'un cercle, un rectangle, un segment... Ceux-ci sont représentés par des formules mathématiques (un rectangle est défini par deux points, un cercle par un centre et un rayon, une courbe par une équation, ...). Une image vectorielle sera toujours nette quelle que soit sa taille contrairement à une image bitmap qui finira par se pixeliser. |
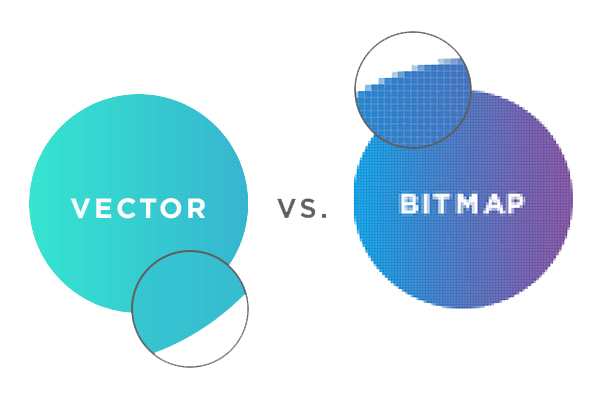
et d'une image bitmap. |
Module PIL (ou pillow) de python
Pour manipuler une image en python, la bibliothèque PIL est parfaitement adaptée. Elle prend en charge une trentaine de formatS d'image bitmap.
from PIL import ImageVoici quelques objets et méthodes utiles de la bibliothèque PIL pour réaliser l'exercice. La documentation complète est accessible sur : Pillow (PIL Fork)
img = Image.open("mon-image.jpg") # Crée un objet img à partir d'un fichier
img.show() # Affiche l'image
img.save('mon-image-v2.jpg', 'jpeg') # Sauvegarde une copie de l'image au format JPEG
largeur, hauteur = img.size # Extrait la largeur et la hauteur en pixel
pix = img.load() # Charge la matrice de pixel
Les variables img et pix sont des instances
d'objets définies dans la bibliothèque PIL. Il s'agit, respectivement d'un
objet image, disposant de nombreuses méthodes (voir documentation), et
d'une matrice contenant tous les pixels de l'image, obtenue grâce à la
méthode load() appliquée à notre objet image.
Il est
possible depuis la matrice d'accéder à un pixel de l'image grâce à
l'instruction pix[x, y] où `x` et `y` sont les coordonnées du
pixel tel que `x in [0, text(largeur)[` et `y in [0, text(hauteur)[`. Le
pixel de coordonnées `(0, 0)` est situé en haut à gauche.
Un pixel
est un tuple de trois entiers appartenant à `[0, 255]` et correspondant
respectivement au niveau de rouge, de vert et de bleu du pixel.
Application
L'objectif de cet exercice est de programmer la rotation d'une image d'un quart de tour avec une fonction récursive. Cette méthode permet d'avoir un coût en mémoire constant en modifier l'image sur elle-même. Pour simplifier le problème, on considère une image carrée dont la largeur en pixel est une puissance de 2. L'idée est de diviser l'image en quatre carrés toujours plus petits jusqu'à atteindre un pixel puis de déplacer ces carrés pour effectuer la rotation.
|
|
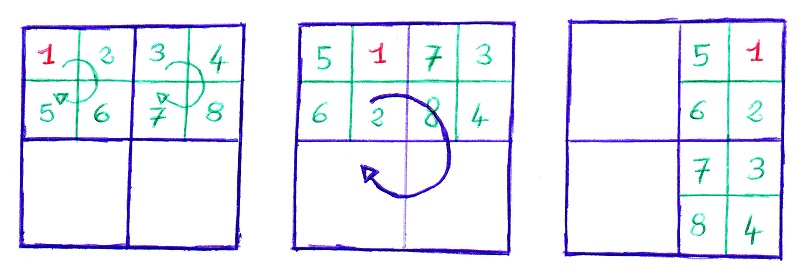
|
1. Définir la fonction privée
_rotation(pix, x, y, n) qui réalise
la rotation de la portion de l'image comprise entre les pixels de
coordonnées `(x, y)` et `(x+n, y+n)`. Pour
simplifier le problème, on considère une image carrée
dont la largeur en pixel est une puissance de 2.
def _rotation(pix, x, y, n):
if n == 1: # Cas de base
return
...
else: # Cas récursifs
# Division en quatre sous-régions
n = n//2
_rotation(pix, x , y , n) # portion supérieure gauche
_rotation(pix, x+n, y , n) # portion supérieure droite
_rotation(pix, x , y+n, n) # portion inférieure gauche
_rotation(pix, x+n, y+n, n) # portion inférieure droite
# Rotation des quatres sous-régions.
...
# Rotation des quatres sous-régions.
for i in range(x, x+n):
for j in range (y, y+n):
pix[i+n, j], pix[i+n, j+n], pix[i, j+n], pix[i,j] = pix[i,j], pix[i+n, j], pix[i+n, j+n], pix[i, j+n]
2. Définir la fonction
rotation(img) qui réalise la
rotation à 90° de l'image en prenant comme argument l'objet
img.
def rotation(im):
pix = im.load()
largeur, hauteur = im.size
_rotation(pix, 0, 0, largeur)
Programmation dynamique
Le contexte
La programmation dynamique apparaît comme pratique de résolution de problèmes mathématico-logistiques et de planification dans les années fin 40 - début 50 du XXème siècle ; plus précisément, elle est formalisée par Richard Bellman entre 1950 et 1953 : l'adjectif «dynamique» a été choisi pour décrire les aspects suivants :
- plusieurs étapes
- dépendance du temps
Bellman a témoigné l'avoir choisi, en plus du côté descriptif d'actions spécifiques dans le temps, pour son aspect vendeur, lui servant de «parapluie pour ses activités» ; activités fort utiles et fécondes. C'est un exemple historique de «coup marketing» qu'un chercheur a été contraint d'employer pour mener d'autres activités qui s'avèrent indispensables aujourd'hui.
Description de la méthode - Exemple avec la suite de Fibonacci
La méthode diviser pour régner scinde un problème en sous-problèmes, souvent indépendants, qu'on résout récursivement, puis la combinaison des solutions obtenues permet de résoudre le problème initial. Cependant, elle perd grandement en efficacité lorsqu'on résout plusieurs fois le même sous-problème.
print permettant
d'obtenir l'historique des appels de cette même fonction. Tester pour
`n=5` et `n=50`.
def fibo(n) :
print("APPEL : fibo("+str(n)+")")
if n <= 1:
return n
else:
return fibo(n-2) + fibo(n-1)|
Si l'on représente les appels récursifs de l'appel `fibo(5)` comme un
graphe, on obtient : Ce graphe (considérons le comme non-orienté à priori) n'étant pas un arbre, certains résultats sont calculés plusieurs fois. |
|
La programmation dynamique consiste alors à stocker les valeurs des sous-problèmes, dans un tableau, pour éviter les recalculs. Selon la direction dans laquelle on lit le graphe, on a deux méthodes dont voici les algorithmes :
|
Méthode ascendante (bottom-top) des plus petits problèmes vers les plus grands |
Méthode descendante (top-bottom) des plus grand problèmes vers les plus petits |
|---|---|
fonction fibonacci(n)
F[0] = 0
F[1] = 1
pour tout i de 2 à n
F[i] = F[i-1] + F[i-2]
retourner F[n]
|
fonction fibonacci(n)
si F[n] n'est pas défini
si n = 0 ou n = 1
F[n] = n
sinon
F[n] = fibonacci(n-1) + fibonacci(n-2)
retourner F[n]
|
1 - Implémenter ces deux approches en python et comparer leur efficacité.
2 - Comparer la complexité des trois solutions ; pour l'implémentation, on pourra utiliser :
import time
start = time.time()
# choses à faire
end = time.time()
print("DURÉE = "+str(end-start)+" s")-
les résultats intermédiaires peuvent être stockés dans une liste
(par exemple
res) ; pour modifier cette liste depuis une fonction, il faut la déclarer variable globale dans la fonction avec :global res. -
Noneetis Nonepermettent de modéliser et de tester des emplacements «vides» dans les listes.
# -*- coding: utf-8 -*-
import time
def fibo(n) :
if n <= 1 :
return n
return fibo(n-2) + fibo(n-1)
def fiboasc(n) :
res = [0, 1]
for k in range(2, n+1) :
res.append(res[k-2] + res[k-1])
return res[n]
def fibodesc(n, res={}) :
if not n in res.keys():
if n <= 1 :
res[n] = n
else :
res[n] = fibodesc(n-2, res) + fibodesc(n-1, res)
return res[n]
# MAIN -----------------------------------------------------
n = 20 # À faire varier !
for fct in [fibo, fiboasc, fibodesc]:
start = time.time()
rep = fct(n)
end = time.time()
dt = (end - start)*1000 # En millisecondes
print(fct.__name__+"("+str(n)+") = "+str(rep) + " ("+str(dt)+" ms)")
Distance de Levenshtein
Deux chaines de caractères, st1 et st2 étant
données, la distance de Levenshtein, aussi nommée
distance d'édition, est le nombre minimal de modifications, chacune d'un
seul caractère, permettant de transformer st1 en
st2. Par modification d'un seul caractère, on entend :
- Remplacer un caractère par un autre ;
- Insérer un caractère ;
- Effacer un caractère.
Voir la vidéo de Graphikart : Distance de Levenshtein.
On peut calculer la distance de Levenstein de la manière suivante :
def lev(st1, st2) :
if not st1: # si st1 est vide
return len(st2)
elif not st2: # si st2 est vide
return len(st1)
else :
subst = int( st1[-1] != st2[-1] )
# subst vaut 1 si les derniers caractères de st1 et st2 sont
# différents, et vaut 0 si ce sont les mêmes.
return min([lev(st1[:-1], st2 ) + 1, # insertion d'un char st1 -> st2
lev(st1 , st2[:-1]) + 1, # suppression d'un char st1 -> st2
lev(st1[:-1], st2[:-1]) + subst]) # remplacement ou non d'un char st1 -> st2
- Tester cet algorithme pour des cas simples : "Bonjour" et "Bonsoir", "buse" et "écluse"... En l'absence d'un cluster de supercalculateurs refroidis dans l'azote liquide, on devrait observer des difficultés de calcul importantes dès que l'on approche la dizaine de caractères.
- Quelle est la complexité de cet algorithme ?
Pour dynamiser cet algorithme, on va utiliser le fait que
lev(st1,st2) == lev(st1.reverse(),st2.reverse()) : en effet,
en inversant l'ordre (sans les mélanger) des deux chaînes, on obtient la
même distance ; en alliant ce fait à une logique de programmation
dynamique bottom-top, on organise les calculs selon un tableau à double
entrée (st1 sur les lignes et st2 pour les
colonnes) :
| ∅ | m | a | i | r | e | |
| ∅ | ||||||
| m | ||||||
| è | a | b | ||||
| r | c | x | ||||
| e |
x = minimum(b+1, c+1, a+subst) où
subst vaut 1 si les derniers caractères ajoutés aux
chaînes sont les différents, et 0 s'ils sont les mêmes.| ∅ | m | a | i | r | e | |
| ∅ | 0 | 1 | 2 | 3 | 4 | 5 |
| m | 1 | 0 | 1 | 2 | 3 | 4 |
| è | 2 | 1 | 1 | 2 | 3 | 4 |
| r | 3 | 2 | 2 | 2 | 2 | 3 |
| e | 4 | 3 | 3 | 3 | 3 | 2 |
#!/usr/bin/env python
# -*- coding: utf-8 -*-
st1 = "Mère"
st2 = "Maire"
l1, l2 = len(st1), len(st2)
mat = [[col for col in range(l2+1)]]+[[li]+l2*[None] for li in range(1,l1+1)]
for li in range(1, l1+1) :
for col in range(1, l2+1) :
subst = int(st1[li-1] != st2[col-1])
mat[li][col] = min(mat[li-1][col] + 1, mat[li][col-1] + 1, mat[li-1][col-1] + subst)
[print(el) for el in mat]
print("\nDonc :\nlev({}, {}) = {}".format(st1,st2,mat[l1][l2]))
Problème du rendu de monnaie

L'objectif est, à partir d'un système de monnaie, de trouver comment
rendre une somme de façon optimale, c'est-à-dire avec le moins de
pièces et de billets possible. Le système de monnaie européen est :
`[0.01, 0.02, 0.05, 0.10, 0.20, 0.50, 1, 2, 5, 10, 20, 50, 100, 200, 500]`
Rappel : En 1ère nous avons vu la stratégie gloutonne pour résoudre ce problème. L'idée de cet algorithme était assez intuitive et consiste, à chaque étape, à faire le choix qui semble le plus optimal. C'est-à-dire, pour le problème du rendu de monnaie, de toujours choisir la plus grande valeur possible pour attindre la valeur souhaitée. Cette stratégie est effectivement optimale quand le système de monnaie l'est aussi. C'est le cas de la monnaie européenne mais pour d'autre système de monnaie, l'algorithme glouton n'est plus optimal.
-
Montrer qu'avec le système
[1, 3, 4], l'algorithme glouton ne donne pas le résultat optimal. On pourra essayer de rendre la monnaie sur une somme de 6. - On veut rendre la monnaie sur une somme de 6. Dessiner un arbre dont la racine est 6, dont chaque nœud a 3 fils correspondant à l'action de rendre 1, 3 et 4 sur la somme indiquée dans le nœud considéré.
-
***Implémenter en Python un algorithme récursif de rendu de monnaie
donnant le nombre de pièces minimal si le rendu est
possible (l'algorithme doit juste donner le nombre de pièces et pas
la décomposition de la somme ; cette dernière option est réalisable,
mais encore plus technique (****)).
Sinon : examiner et expliquer le fonctionnement du programme donné en correction. - Tester ce programme récursif. Est-il efficace ? Pourquoi ?
- Pour l'algorithme glouton, on obtient 3 pièces : 6 = 4 + 1 + 1. La solution optimale est 6 = 3 + 3.
- On voit beaucoup de motifs se répéter : ils donneront lieu à des calculs qui se répètent s'ils sont implémentés...
-
#!/usr/bin/env python # -*- coding: utf-8 -*- somme = 79 sys = (2,5,10,50,100) n = len(sys) oo = float("inf") # j'invoque l'infini L(・o・)」 def renduMonnaie(somme, sys) : if not somme : # si la somme vaut 0 return 0 else : mini = oo for k in range(n) : if sys[k] <= somme : nb = 1 + renduMonnaie(somme-sys[k], sys) if nb < mini : mini = nb return mini print(renduMonnaie(somme, sys)) - Le programme est très lent, il est en 'O((#sys)^n)' (cf la boucle for) !
Pour le rendre plus dynamique, on va stocker les résultats obtenus dans un tableau de taille somme+1 (de 0 à somme).
#!/usr/bin/env python
# -*- coding: utf-8 -*-
somme = 79
sys = (2,5,10,50,100)
n = len(sys)
oo = float("inf") # j'invoque l'infini L(・o・)」
res = (somme+1)*[None] # résultats déjà calculés
def renduMonnaie(somme, sys, res) :
if not somme : # si la somme vaut 0
return 0
elif res[somme] is not None :
return res[somme]
else :
mini = oo
for k in range(n) :
if sys[k] <= somme :
nb = 1 + renduMonnaie(somme-sys[k], sys, res)
if nb < mini : # si on trouve...
mini = nb
res[somme] = mini # ... on stocke !
return mini
print(renduMonnaie(somme, sys, res))
Recherche textuelle
La recherche d'une sous-chaîne de caractères dans une plus grande chaîne de caractère est un grand classique en algorithmique. Ces algorithmes sont natommant utilisés en bioinformatique à propos de la recherche de séquence ADN. L'ADN est une molécule en double hélices qui est constituée d'un enchaînement de quatre nucléotides différents : A, C, G et T pour Adénine, Cytosine, Guanine et Thymine. Cette suite de nucléotides code l'information pour la synthèse des protéines essentielles au fonctionnement de notre organisme. Le séquençage de l'ADN à l'origine de la révolution de la recherche en génétique, consiste à obtenir la suite des nucléotides et à y rechercher des motifs correspondant à différents gènes. L'optimisation des algorithmes de recherche est un enjeu majeur pour la recherche génétique.
- La chaîne de caractère recherchée est appelée le motif ou la clé.
- La chaîne de caractère dans laquelle s'effectue la recherche est appelée la séquence ou le texte.
- Chaque apparition du motif dans le texte est appelée une occurrence.
Algorithme naïf (Algorithme par force brute)
L'approche naïve pour la recherche textuelle est d'effectuer une comparaison du motif avec la séquence en commençant par la gauche et en comparant les caractères un par un de gauche à droite puis en décalant le motif vers la droite caractère par caractère. On parle ici de force brute car nous testons ainsi toutes les possibilités, ce qui est la caractéristique des algorithmes par force brute.
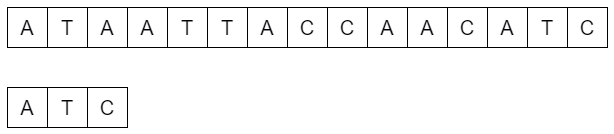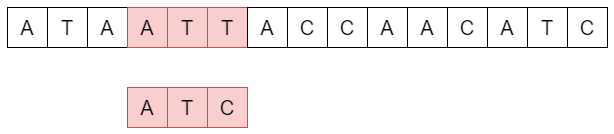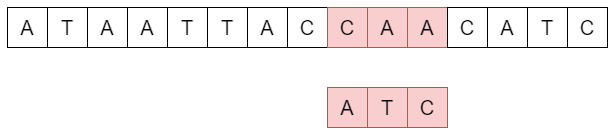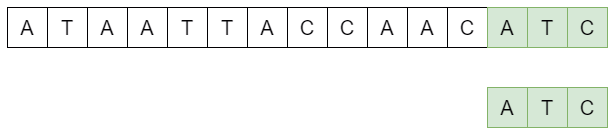
def comparer(texte, motif):
for i in range(len(texte) - len(motif) +1):
if texte[i:i+len(motif)] == motif:
print(texte[:i]+"["+motif+"]"+texte[i+len(motif)+1:])
return i
return False
texte = "AAAGTCGGTCCCGTAGCTGATGTCCC"
motif = "GTCCC"
print(comparer(texte, motif))
def comparer(texte, motif):
liste = []
for i in range(len(texte) - len(motif) +1):
if texte[i:i+len(motif)] == motif:
liste.append(i)
# print(texte[:i]+"["+motif+"]"+texte[i+len(motif)+1:])
return liste
texte = "AAAGTCGGTCCCGTAGCTGATGTCCC"
motif = "GTCCC"
print(comparer(texte, motif))Algorithme de Boyer-Moore
L'algorithme de Boyer-Moore, optimise l'algorithme naïf en diminuant le nombre de comparaisons par l'élimination de celles qui sont inutiles.
Considérons le motif : CGGCAG à rechercher dans
la
séquence : CAATGTCTGCACCAAGACGCCGGCAGGTGCAGACCTTCGTTATAGG
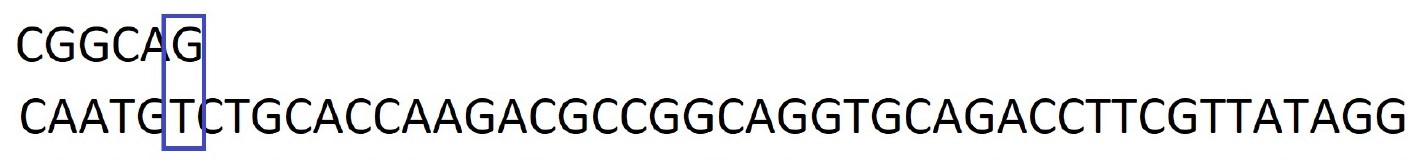
Etape 1 : On commence à placer le motif sur la gauche de la séquence.
Première idée de l'algorithme de Boyer-Moore : Comparer le motif à
la séquence en partant de la droite.
Deuxième idée : Sachant que le
motif ne contient pas la lettre T, il est possible de
décaler tout le motif pour le placer après la lettre T de
la séquence.
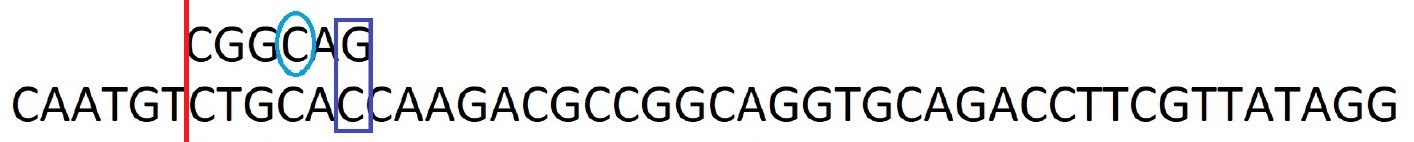
Etape 2 : On recommence les comparaisons par la droite. Troisième idée : Le caractère C ne correspond pas il est ailleurs dans le motif. On décale le motif jusqu'à faire correspondre le caractère C.
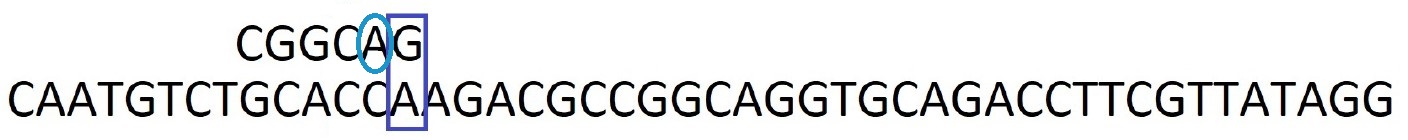
Etape 3 : On recommence les comparaisons par la droite. Encore une fois, le caractère A ne correspond pas mais il est ailleurs dans le motif. On décale le motif pour faire correspondre le caractère A.
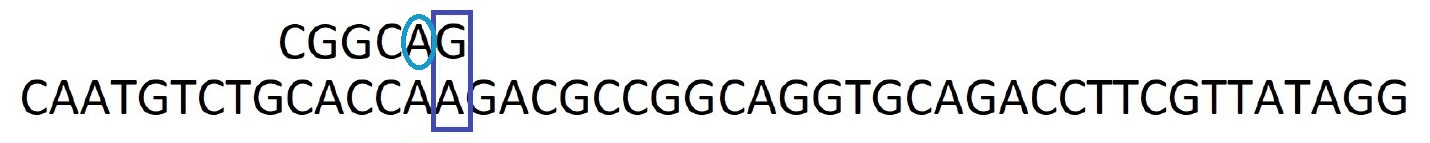
Etape 4 : On recommence les comparaisons par la droite. Encore une fois, le caractère A ne correspond pas mais il est ailleurs dans le motif. On décale le motif pour faire correspondre le caractère A.
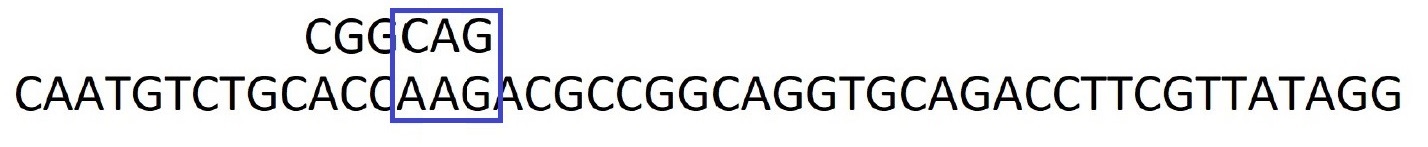
Etape 5 : On recommence les comparaisons par la droite. Les caractères G et A correspondent mais pas le caractère A suivant. Sachant qu'il n'y a plus de A dans le motif, on peut le décaler au delà de ce caractère A de la séquence.

Etape 6 : Et ainsi de suite jusqu'à trouver une occurrence. On note alors sa position dans la séquence.
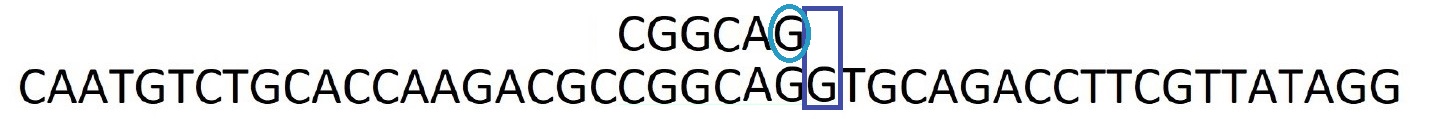
Etape 7 : Après avoir trouver une occurrence, on regarde le caractère suivant dans la séquence, ici c'est un G. Sachant qu'il y a un G dans le motif, on décale le motif pour les faire correspondre.
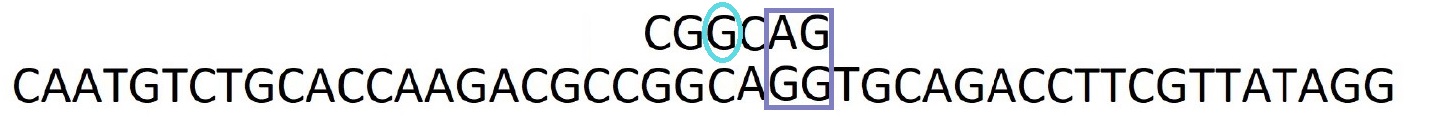
Etape 8 : Et on recommence les comparaisons par la droite ...
Les trois grandes idées de l'algorithme de Boyer-Moore sont donc :
- La comparaison de droite à gauche des caractères du motif et du texte.
- Le décalage du motif de plusieurs crans vers la droite lorsque c'est possible plutôt que de le faire glisser d'un seul caractère à la fois.
- Le pré-traitement du motif afin d'en avoir une bonne connaissance et permettre les grands décalages du motif.
À travers l'exemple précédent, on voit qu'il faut connaître le motif pour effectuer des sauts et faire correspondre une lettre de la séquence à sa première occurrence en suivant dans le motif. Une première étape importante dans l'algorithme sera alors de créer une table de décalage. Cette dernière doit nous dire combien de sauts effectuer dans le cas ou un caractère ne correspondrait pas. Il s'agit d'une table à double entrées : le caractère recherché et la position du caractère du motif qui diffère de la séquence.
|
Position dans le motif du caractère qui diffère |
Nombre de sauts pour atteindre : | ||
| un A | un C | un G | |
| 0 | 0 | ||
| 1 | 1 | 0 | |
| 2 | 2 | 0 | |
| 3 | 0 | 1 | |
| 4 | 0 | 1 | 2 |
| 5 | 1 | 2 | 0 |
assert rechercher("GGC", "TGTCGAGC") == [] # Pas d'occurence
assert rechercher("AGT", "AGTCCGGA") == [0] # Occurence en début
assert rechercher("TGG", "CGATGAAATGG") == [8] # Occurence en fin
assert rechercher("GAA", "GAGAATCGATTTGAACGAA") == [2, 12, 16] # Plusieurs occurences
assert rechercher("nn", "Une bonne connaissance du motif permet les grands décalages.") == [6, 12] # Texte plus long et complexe
assert rechercher("A", "AGTCCGGA") == [0, 7] # Motif d'une lettre
assert rechercher("GCT", "") == [] # Pas de texte
assert rechercher("AGTCCGGA", "AGCCT") == [] # Motif plus long que le Texte
table_decalage permettant de générer cette table à partir
du motif.
def table_decalage(motif):
d = [{} for _ in range(len(motif))]
for j in range(len(motif)): # Parcours du motif
for k in range(j): # Parcours du motif jusqu'à j
if motif[j] != motif[k]: # Si la lettre est différente
d[j][motif[k]] = j - k # Ajoute le nbr de saut pour l'atteindre
return d2 - Reste ensuite à coder l'algorithme de recherche du motif dans le texte en faisant appel à la table de décalage quand un caractère différe. Il faudra traité le cas où le caractère recherché n'existe plus dans le reste du motif et alors réaliser un décalage jusqu'à la fin du motif.
def rechercher(motif, texte):
d = table_decalage(motif)
occ = [] # Indice des occurences
i = 0
while i <= len(texte) - len(motif): # Parcours du texte
k = 0
for j in range(len(motif) - 1, -1, -1): # Parcours du motif
c = texte[i+j] # Caractère de la séquence
if c != motif[j]: # Si la lettre diffère
if c in d[j].keys(): # Si possible
k = d[j][c] # décalage vers la lettre
else: # sinon
k = j+1 # vers la fin du motif
break
if k == 0:
occ.append(i)
k = 1
i += k
return occtime de python.
from time import *
start = time()
algo_naif()
end = time()
print("Algo naïf : "+ str((end-start)*1000)+" ms")
start = time()
algo_BM()
end = time()
print("Algo BM : "+ str((end-start)*1000)+" ms")
Pour aller plus loin : Algorithme KMP
Pour approfondir ce domaine de l'algorithmique de recherche textuelle, sachez que l'outil "principal" est l'automate. Grossièrement, un automate est un graphe orienté dont les arêtes ont été étiquetées :
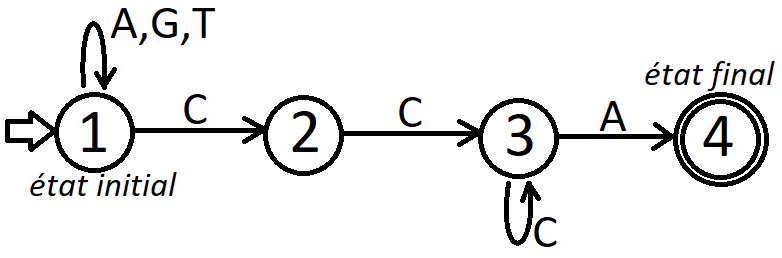
Si vous êtes intéressé, vous pouvez rechercher l'algorithme de Knuth-Morris-Pratt, qui est un autre algorithme de recherche d'un motif dans un texte. Il existe en deux versions, une version où la présence des automates est masquée pour permettre une compréhension de l'algorithme au plus grand nombre, y compris à ceux qui n'ont jamais entendu parler d'automates, et une deuxième version dans laquelle les automates sont présents. Tapez "Algorithme de Knuth-Morris-Pratt" ou "Automate des occurrences" dans votre moteur de recherche préféré pour trouver ces deux versions.
En anglais :
- récursivité : recursion
- fonction factorielle : factorial function
- algorithme diviser pour régner : divide-and-conquer algorithm
- tri fusion : merge sort
- programmation dynamique : dynamic programming